빅데이터 활용 제약바이오연구 소개

차라투(주)

김진섭

2025-07-11

자기소개

회사: 차라투 주식회사(Zarathu Co.,Ltd)

의학연구지원
R 패키지 개발 및 교육
인턴십(연세대 학부생, 의대생/전공의 20명 이상)

경력

의학사, 성균관대학교 (~2009)
예방의학전문의/박사수료,서울대보건대학원 (~2013)
책임, 삼성전자 DMC연구소/무선사업부 (~2016)
대표, 차라투 (2018~)
겸임교수, 성균관대 바이오헬스규제과학과(2022)

jinseob2kim@gmail.com, github.com/jinseob2kim

Executive summary

병원데이터: (1) 연구위해 정리된 (2) 연구위해 정리해야 할

정리된: 개인연구자 엑셀, 레지스트리, RCT
정리 필요: CDW, CDM, 공단/심평원

데이터 정리: R(CPU < RAM)

data.table: 빠른 읽기/쓰기, 환자ID 별 작업, melt/dcast
fst: fst 확장자 통한 가장 빠른 읽기/쓰기
%>% operater: 의식의 흐름대로 코드짜기, parallel::mclapply: 멀티코어

많이 쓰는 통계: logistic, survival, subgroup analysis, 인과추론(PS/IPTW)

자체개발한 jstable, jskm, jsmodule R 패키지, 무료웹 https://openstat.ai

분석결과 공유: 엑셀, PPT, 워드, 웹 애플리케이션: officer/rvg/flextable/shiny

정리된 데이터

연구만을 위해 만들어진 데이터

관심있는 Time(Baseline/1yr/2yr/마지막방문) 별로 변수들이 존재
csv/xlsx/spss/sas, 엑셀파일 여러개, 엑셀시트 여러개
데이터 퀄리티는 보장못함: 결측/오타/밀려쓰기..
연구자 직접 작성, 레지스트리(학회/병원), RCT(연구자주도 임상)

정리 필요한 데이터: Real World Data(RWD)

연구 위해 만들어진 데이터가 아님, 환자가 언제 와서, 어떤 진단 을 받고, 어떤 검사와 치료를 받았는지 단순 나열

CDW/CDM: EMR
공단/심평원: 청구데이터

연구의 각 Time을 정의하고, Time에 해당하는 변수들을 직접 만들어야

나이, 과거력, 과거 약물, 추적관찰 및 질병 발생

CDW

EMR 을 데이터베이스화

특정 조건에 맞는 환자정보를 뽑아낼 수 있음
누가, 언제, 무슨 진단/약/검사 를 했는지 나열

연구시작일은 언제? 결과발생은 언제? 과거력 기준은?

연구자가 직접 하나하나 정의해야

CDM

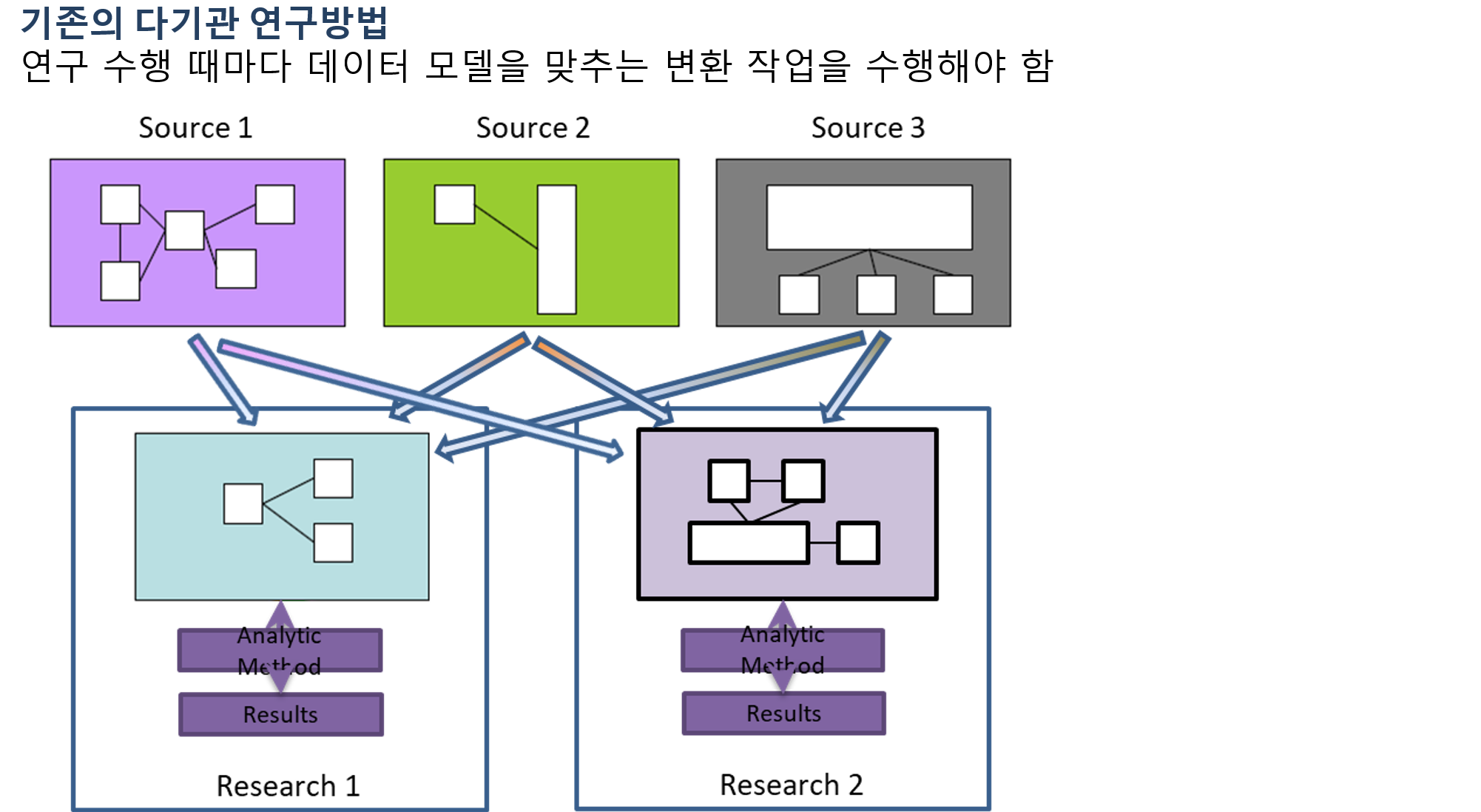
출처: 유승찬교수님 슬라이드.

Why CDM(2)

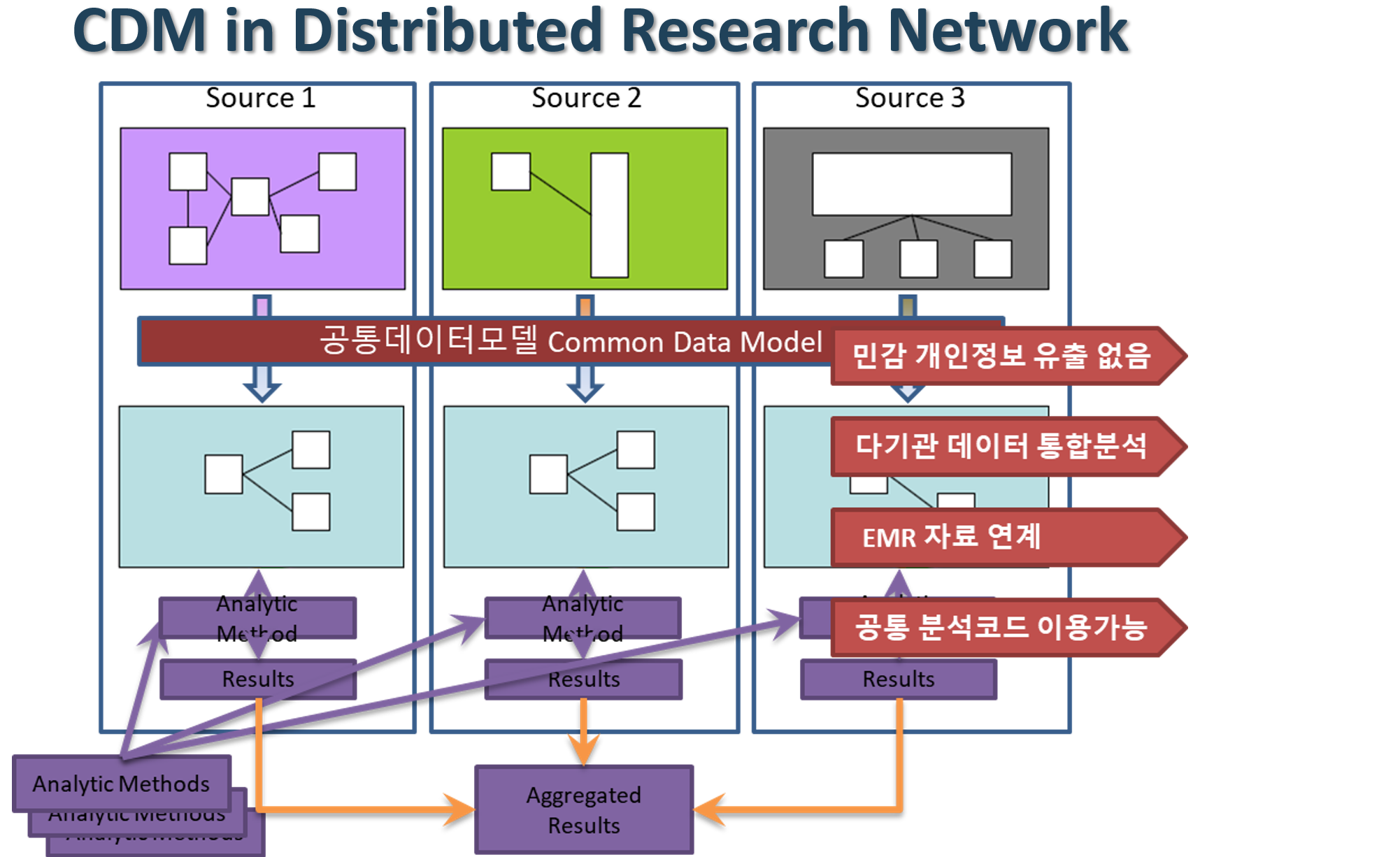
Why CDM(3)

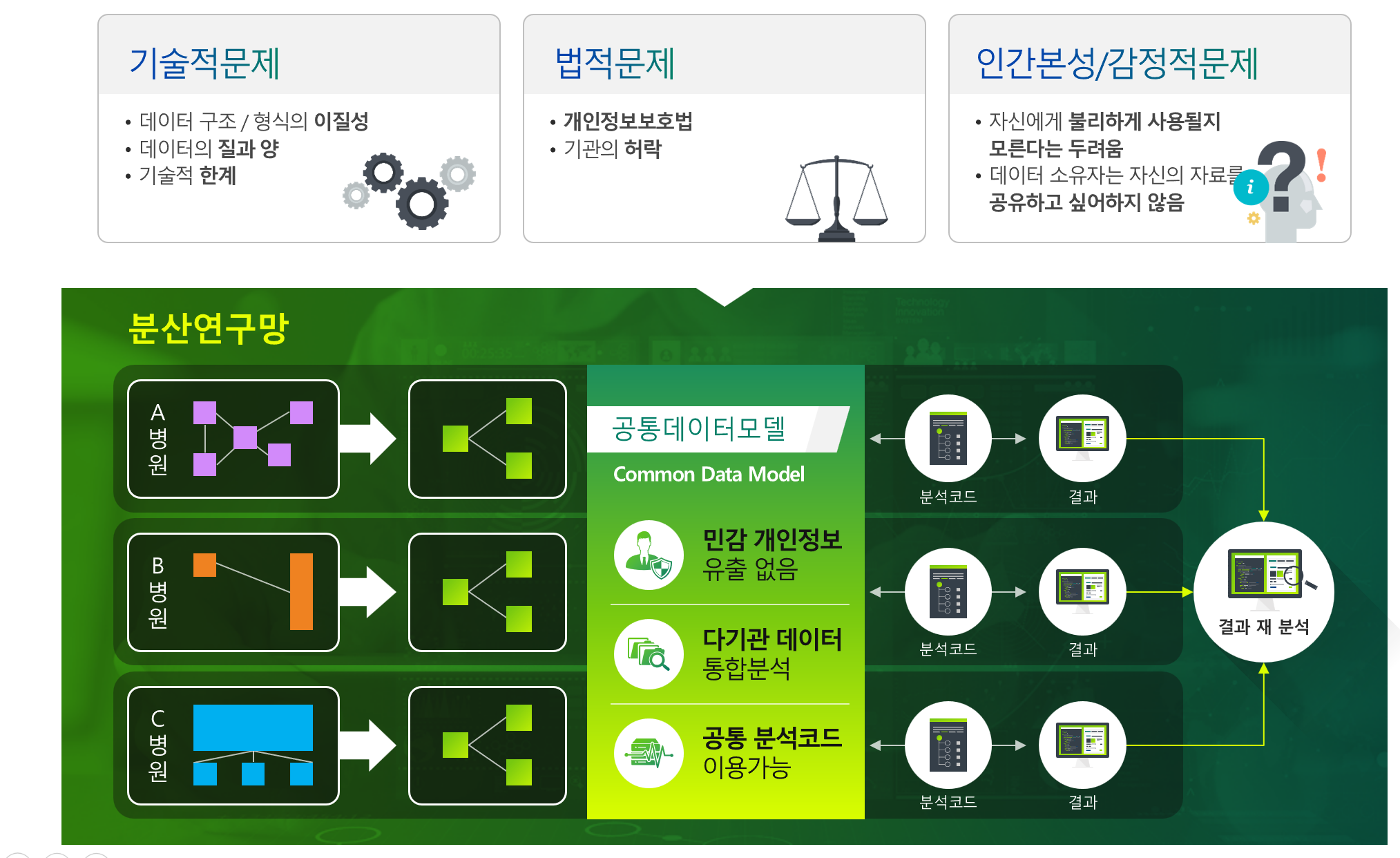
OMOP CDM V6

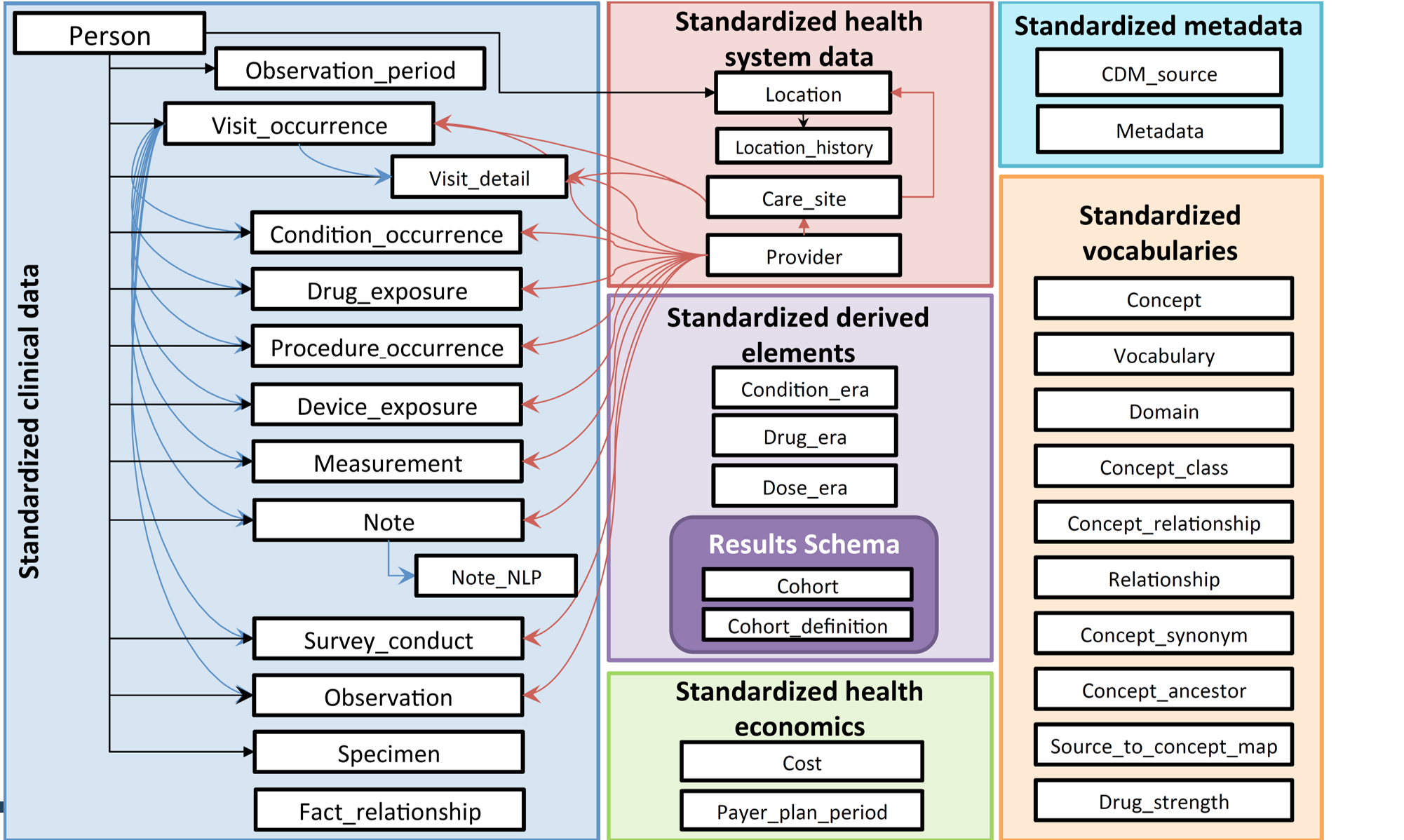
동일한 데이터 구조 뿐 아니라 OMOP 코드라는 공통 의료용어체계를 이용해 물리/논리적 공통모델을 사용함

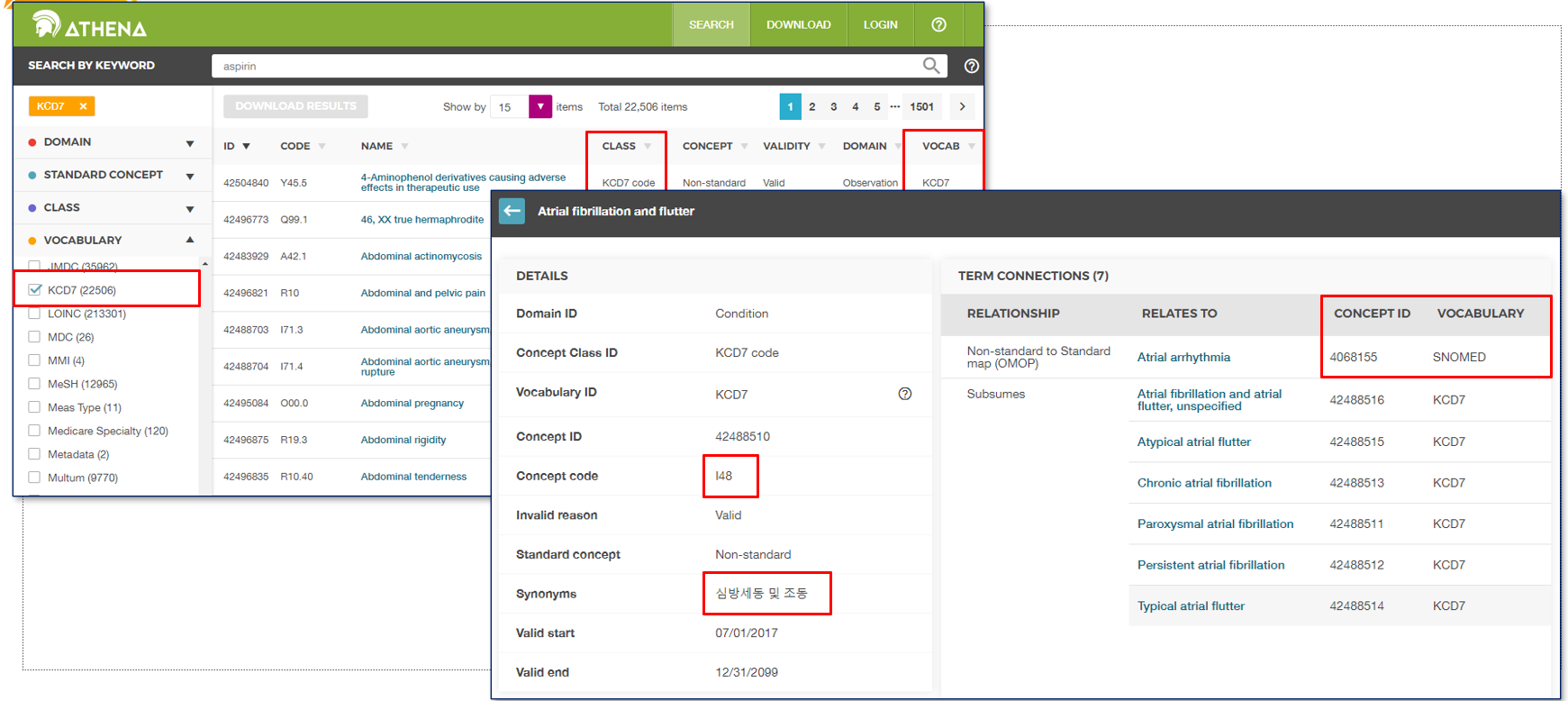
Standardized Vocabulary 예

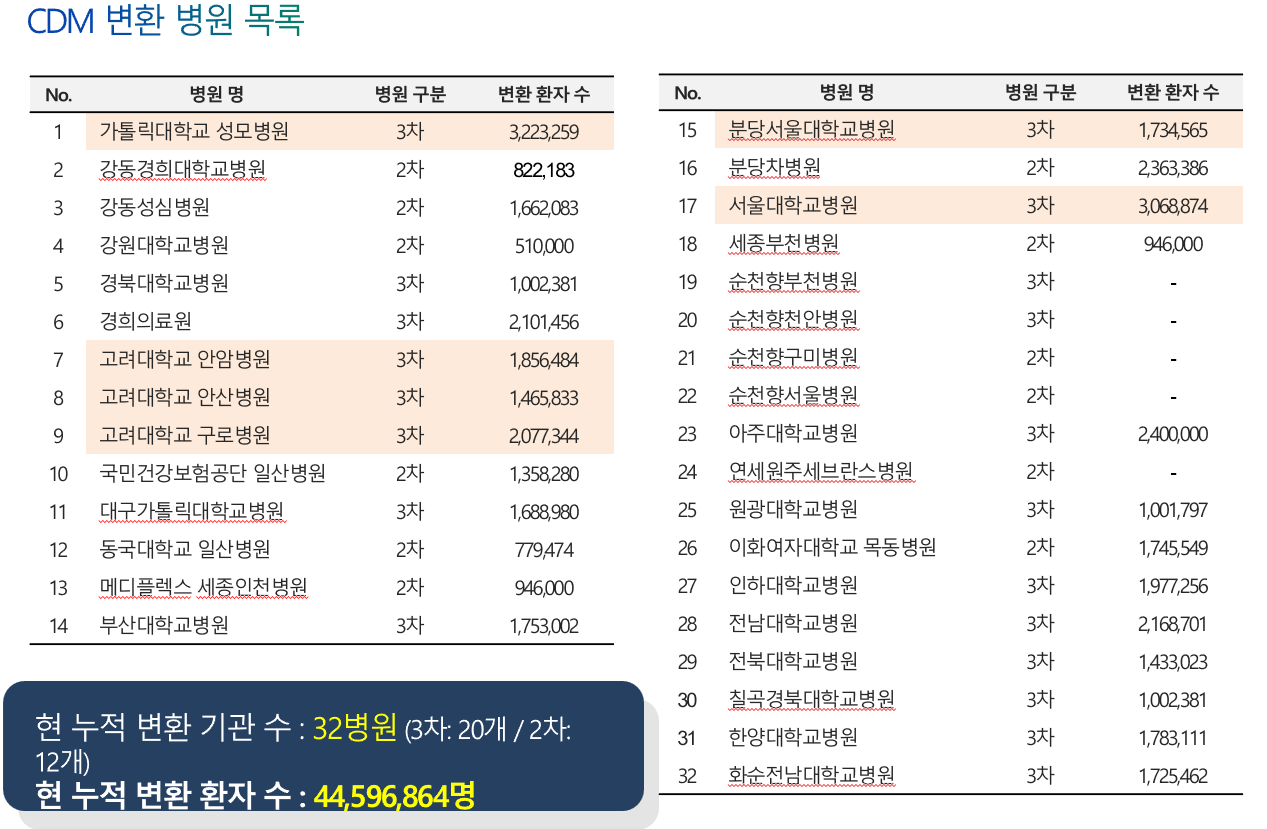
국내 참여 병원

HIRA CDM

R first

CDM 분석 모든과정은 R패키지로 구현됨.

분석코드, 결과도 R패키지

연구설계, 분석방법이 포함된 자체 R패키지가 코드공유 표준.

R패키지를 여러 기관에서 실행

https://github.com/zarathucorp/RanitidineCancerRisk

분석결과는 R Shiny로

실행결과를 R기반 웹애플리케이션으로 표현
분석코드에 웹코드도 포함되어있음.

ATLAS

웹기반 연구설계: R 몰라도 가능

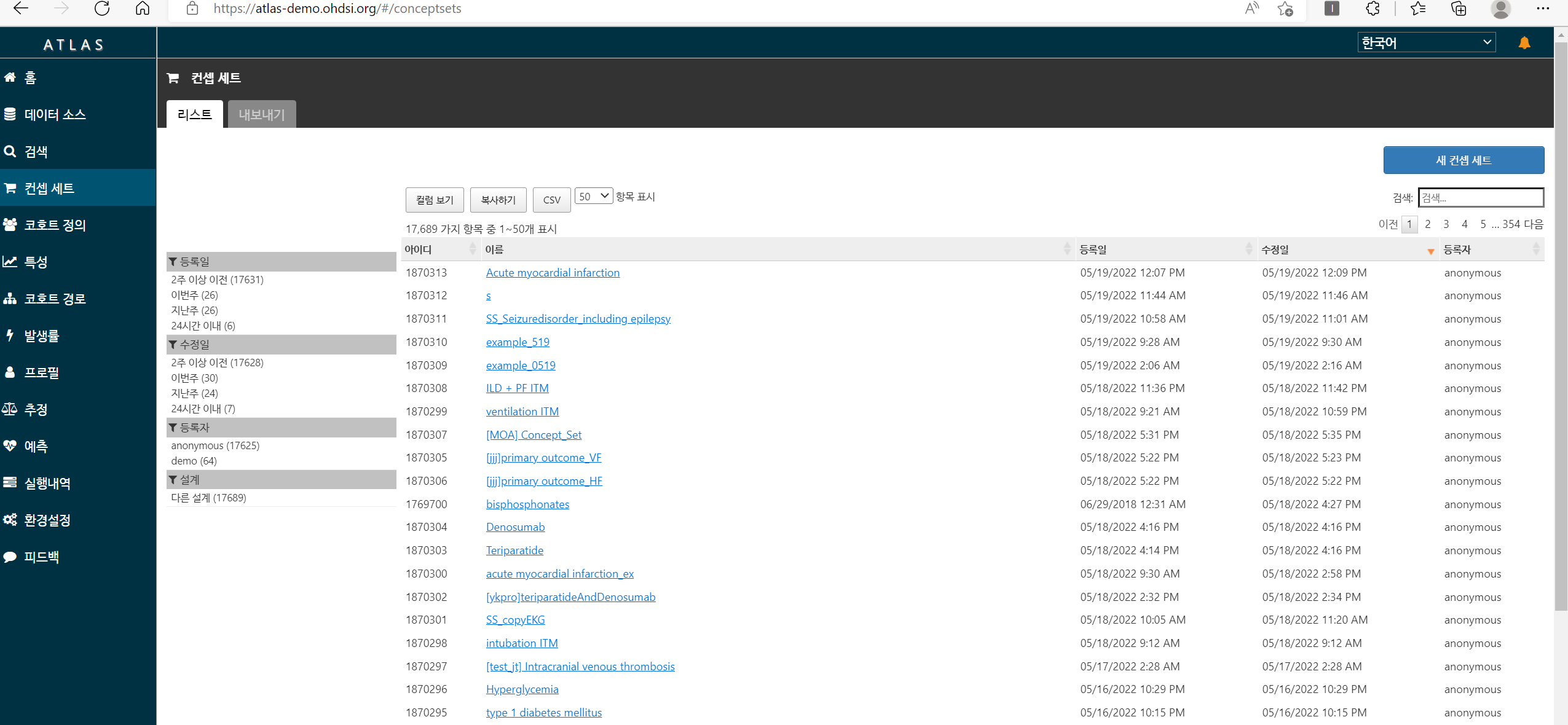
데이터 소스

데이터 선택: 기본정보 제공

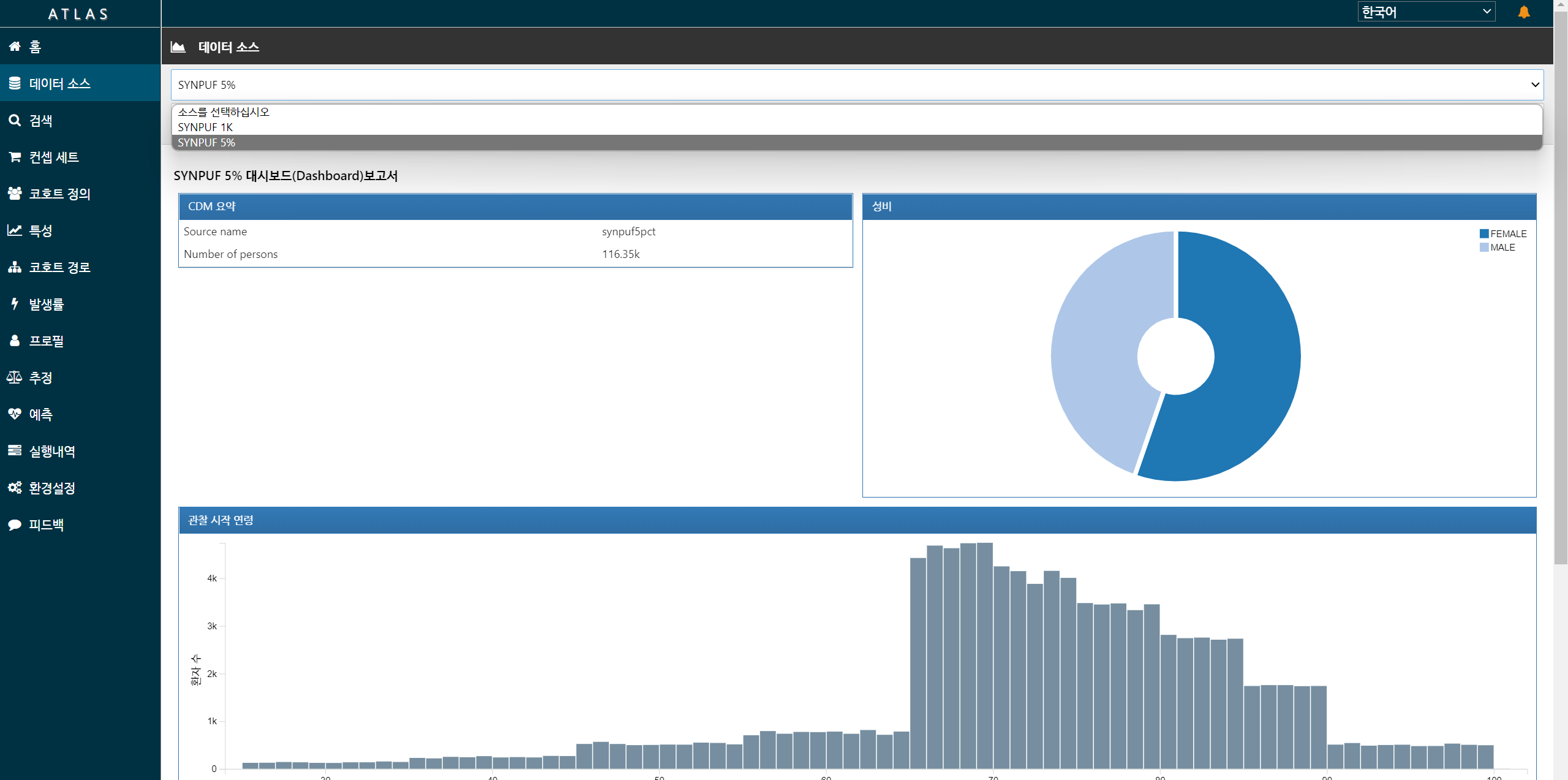
컨셉세트

연구에 이용할 개념 정의 - 예: 고혈압, ACEI, PCI..

사망은 기본으로 있음

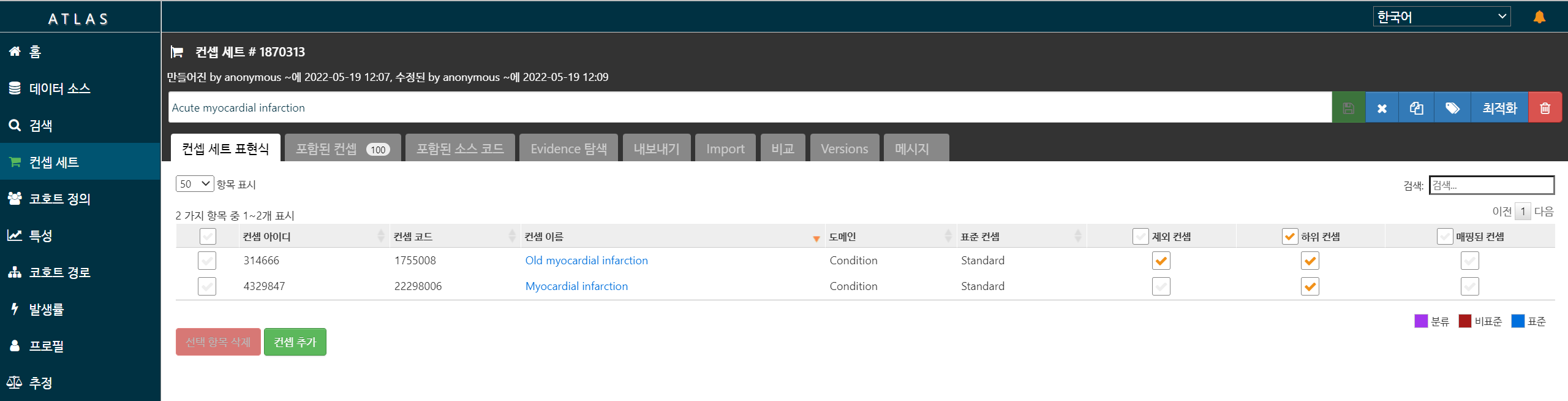
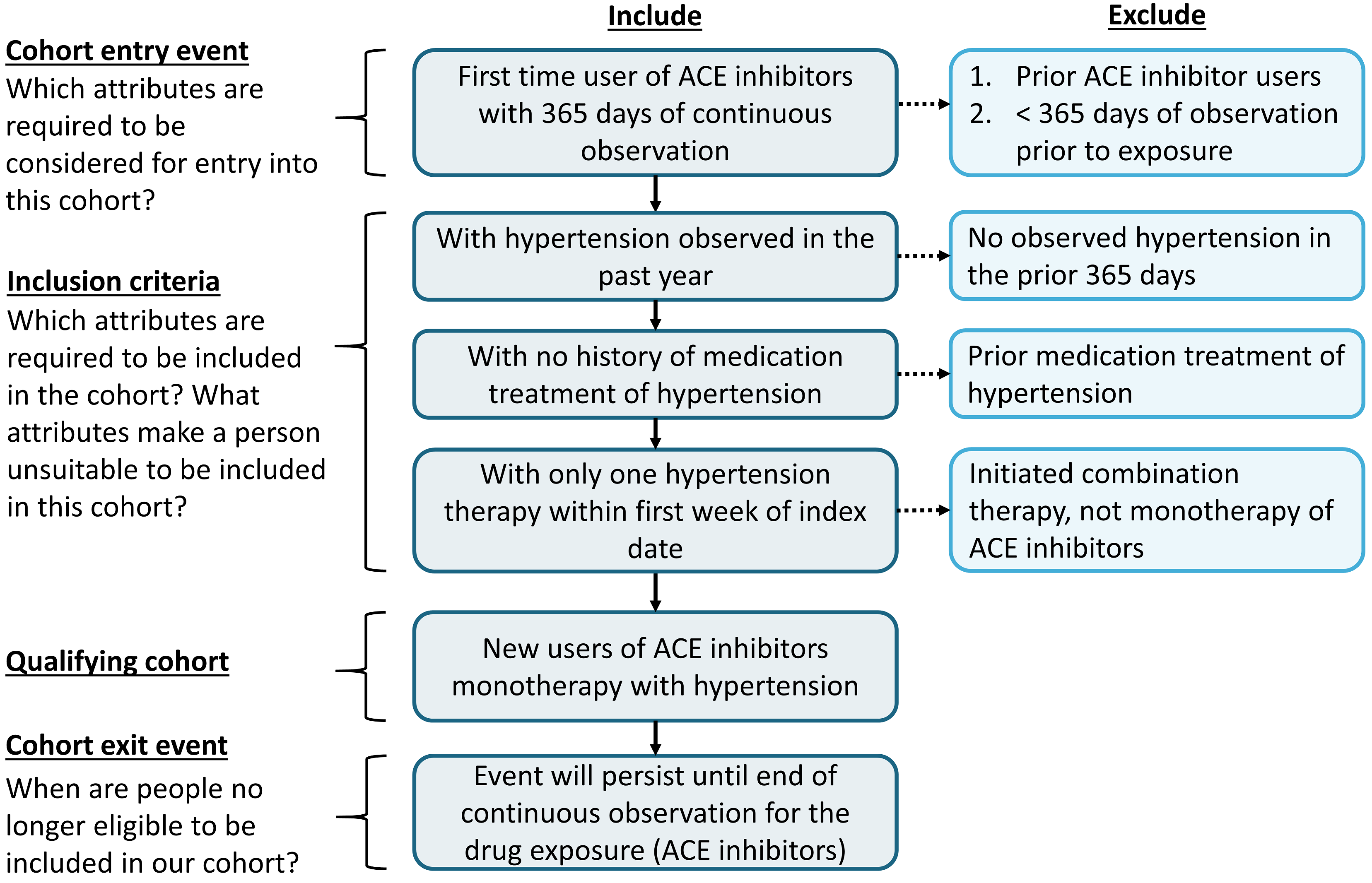
코호트 정의

컨셉세트 이용해 코호트 정의

최소 Target/Control/Outcome 코호트 3개 필요
Negative control 도 필요(자체만들기 or 기본제공)

분석

추정: Logistic/Cox

예측: xgboost, Lasso, 딥러닝

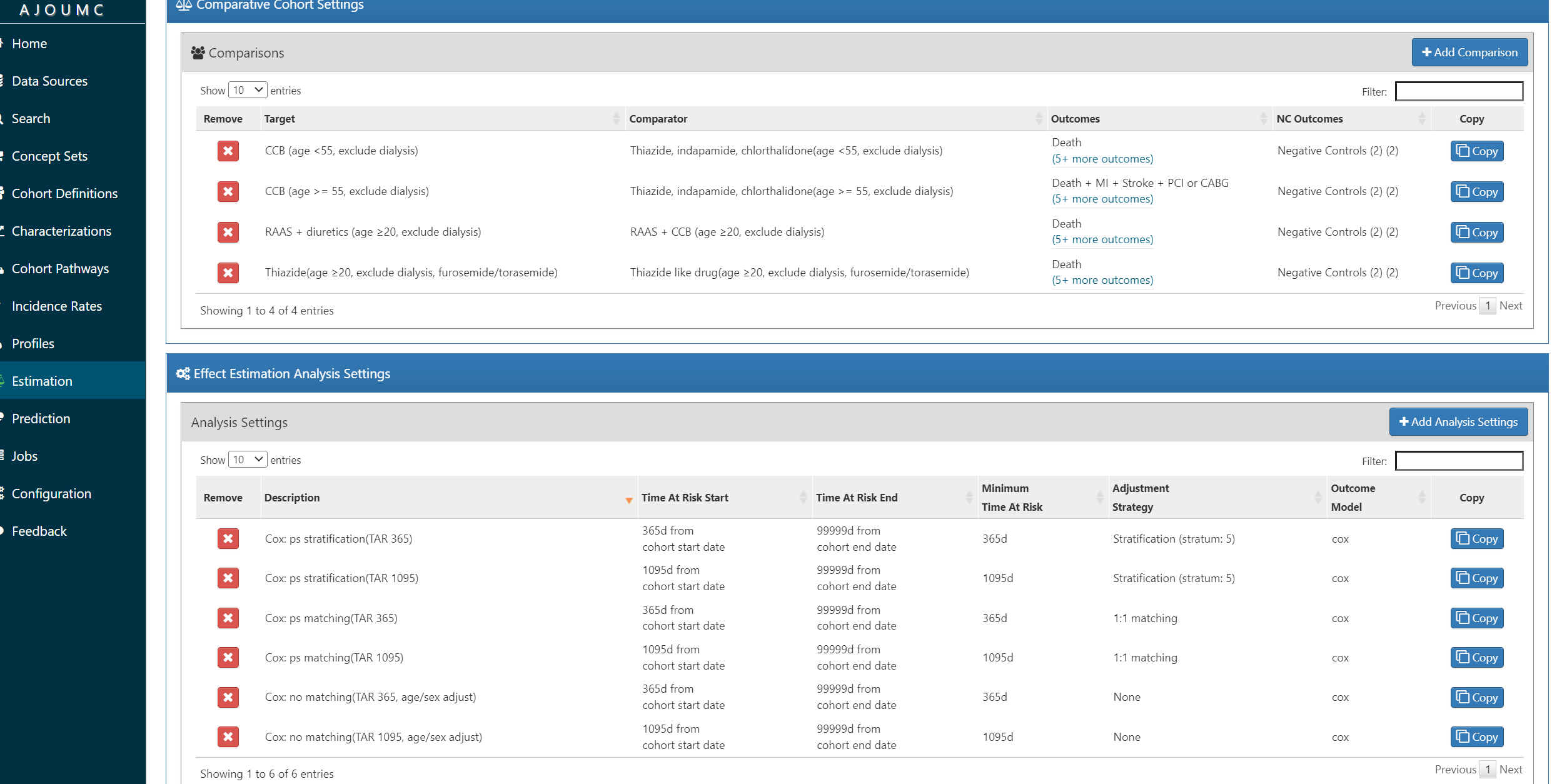
R패키지 다운

컨셉, 코호트, 분석이 모두 포함된 R 패키지 다운로드

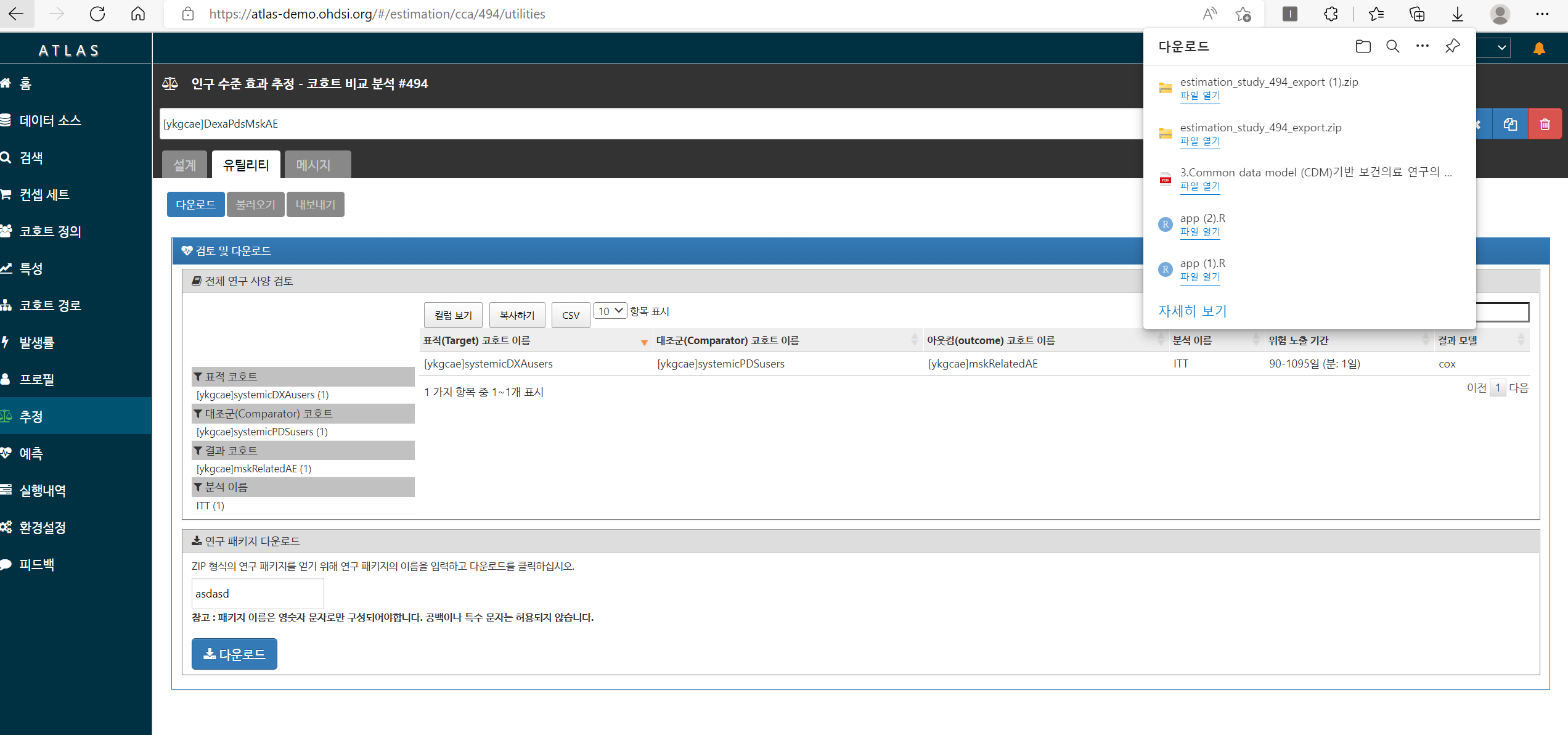
이후 (1)각 병원의 RStudio server 접속, (2)패키지 설치, (3)실행 하여 분석결과 zip 파일 얻음.

Feedernet 이용

가장 쉬운 방법

R코드 안봐도됨.
다기관메타 쉽게 가능(분석할 병원 추가로 끝)

단점

ATLAS 에서 지원하는 분석만 됨. 직접 수정한 R패키지 불가
접근권한 얻은 병원만 분석 가능. 소속, 신분에 따라 다름

분석은 심플하되, 다기관 물량으로 승부하는 컨셉

단계

(1) Feedernet 에서 Atlas, 분석실행 둘다

Atlas에서 지원하는 분석, Feedernet 허가된 데이터만 분석가능

(2) Feedernet/각병원 Atlas로 설계, 분석은 R서버 접속.

Atlas에서 지원하는 분석, 자체 CDM설치병원의 데이터 분석가능

(3) 설계도 R로, 분석도 R서버 접속

자유롭게 분석설계 가능, 자체 CDM 설치병원의 데이터 분석가능

Textbook

공식 교과서: 친절한 예제, 영어버전은 무료공개

공식 유튜브

연구지원경험: 심평원 Covid-19 데이터

한시적 오픈 with CDM버전, 패키지 만들어 심평원 보내면 실행결과만 보내줌.

RAAS vs Other HTN drug in Covid-19

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0248058#pone-0248058-g001

NSAIDs vs AAP in Covid-19

https://www.nature.com/articles/s41598-021-84539-5

강동성심병원

첫 CDM 연구, ATLAS로 패키지만들고 강동성심 DB 접속해 R 실행
Kaplan-meier 그림을 논문용으로 업그레이드

https://onlinelibrary.wiley.com/doi/abs/10.1111/jgh.14983

공단표본코호트 V1

CDM 변환된 공단표본코호트와, 원본 표본코호트 결과 비교

공단표본코호트 V1(2)

CDM 변환된 공단표본코호트 이용

공단표본코호트 V1(3)

CDM 변환된 공단표본코호트 이용

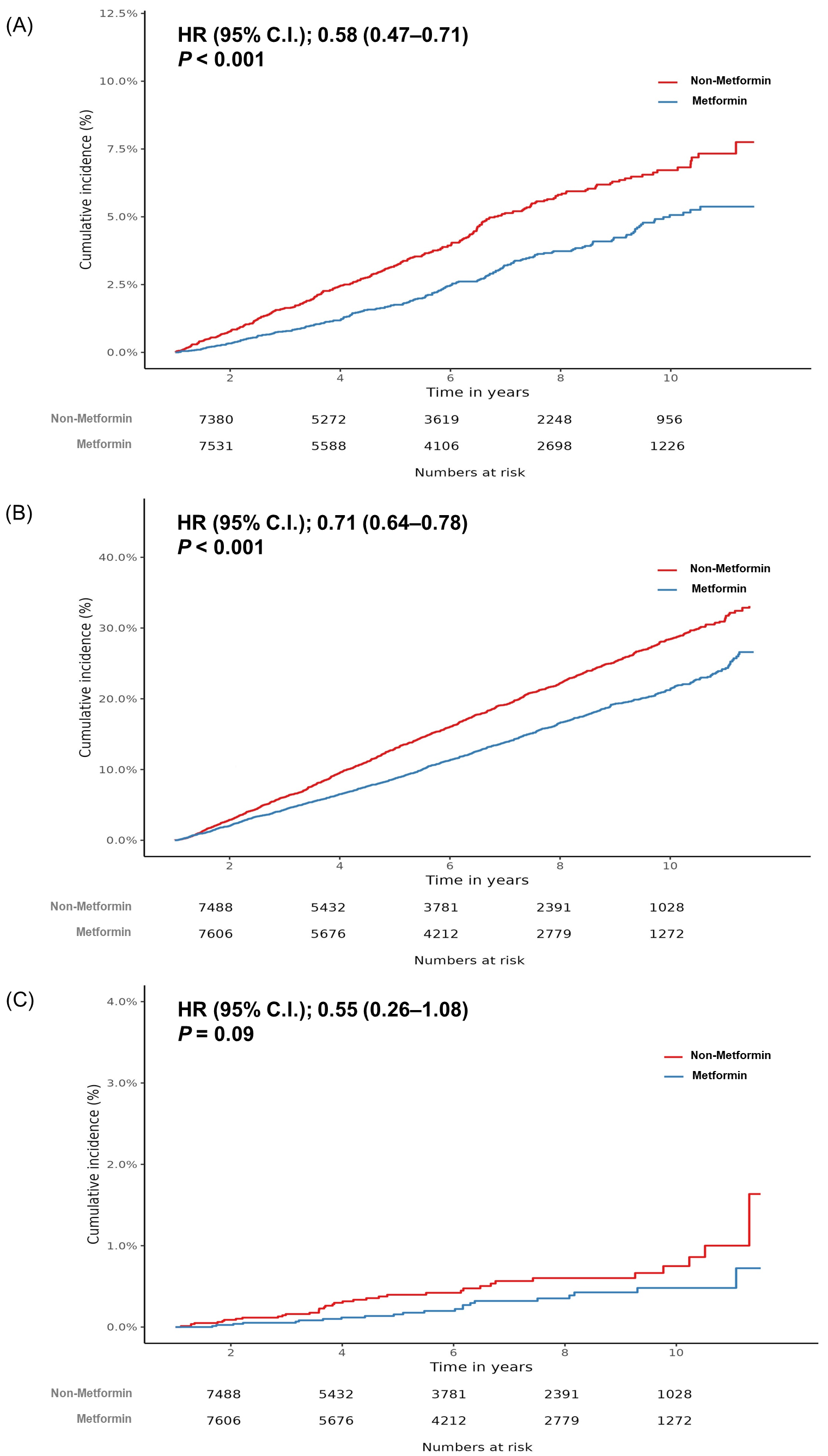
Feedernet 다기관메타

ACEI vs ARB

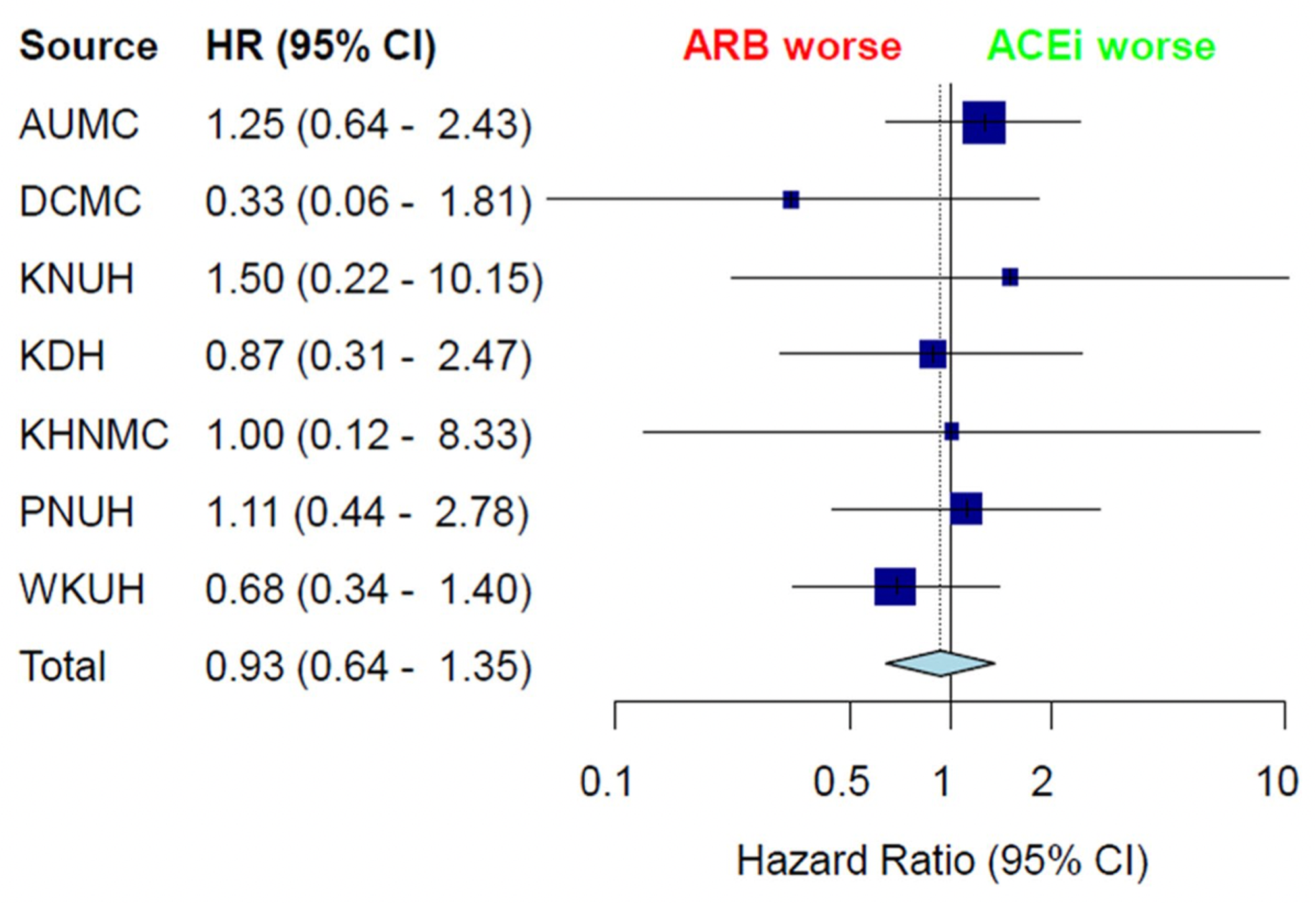
Feedernet 다기관메타(2)

ACEI_ARB vs OtherHTNdrug

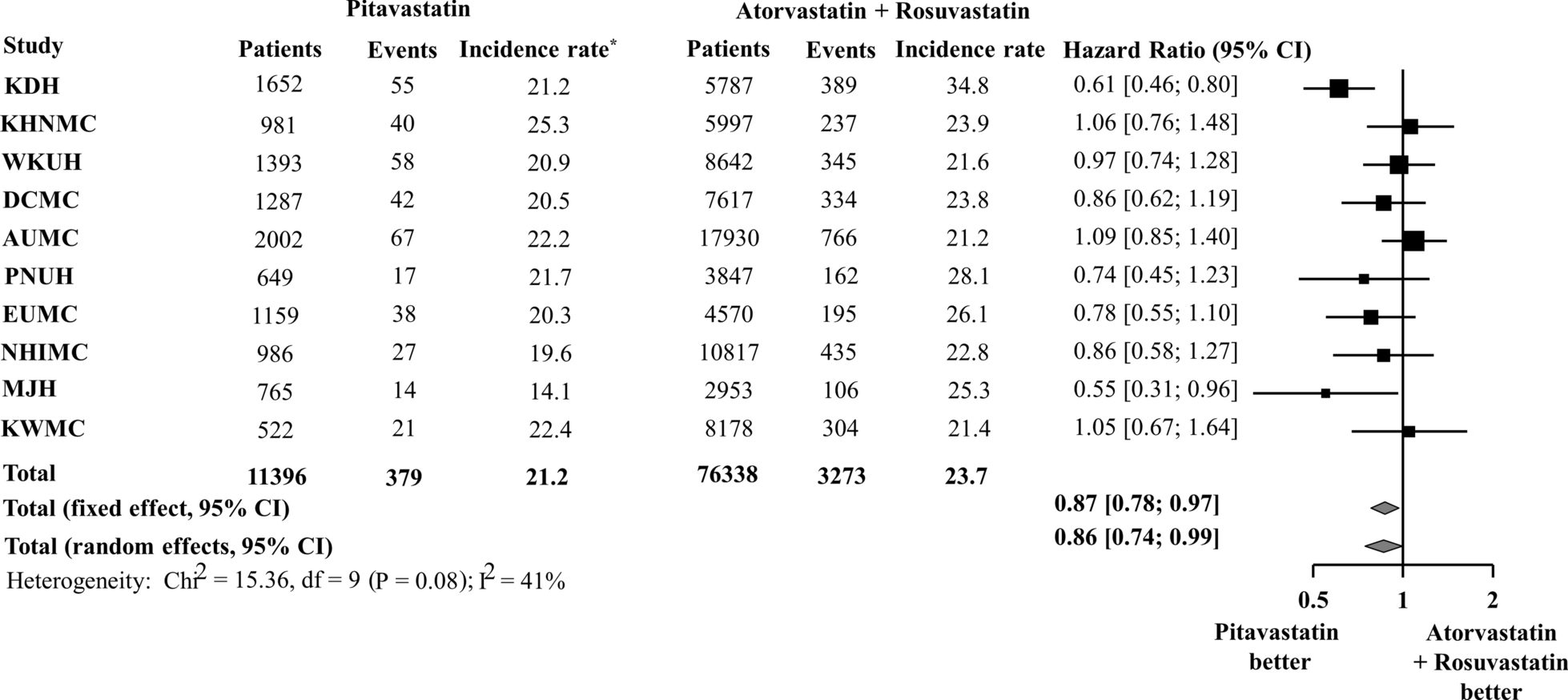
Feedernet 다기관메타(3)

pitavastatin vs other Statin

CDM summary

CDM은 병원들의 데이터를 똑같은 형태로 만든다.
하나의 분석코드로 다기관메타분석 가능
분석 전과정에 R을 이용하나, Feedernet 에서 R없이 기본분석 가능.

공단, 심평원

세계적으로 경쟁력있는 국가빅데이터로 연구활발

BMJ, European Heart Journal 등 최고수준 저널에 게재

전국민의 청구자료 모음

공단은 국가검진자료까지 포함, 특정연구 위해서만 제공하는 변수도 있음
한의, 치의학 데이터 따로 존재

원격(심평원, 공단표본), 분석실방문(공단 맞춤형)

BMJ: 산모 자녀 매칭

경희대학교 의학과 연동건 교수 연구팀(김현진 석사연구원, 하버드의과대학 강지승 박사, 연세대 의과대학 신재일 교수)이 한국 건강보험공단 대규모 의료 빅데이터를 구축해 산모의 임신 중 마약성 진통제 사용과 출산 이후 소아의 신경정신과적 장애의 발병 연관성을 분석했다. 의료 빅데이터를 통해 이를 분석한 연구는 세계 최초의 일이다. 연구 성과는 의학 분야 세계 5대 학술지로 꼽히는영국의학저널(BMJ) 에 게재됐다.

성균관대학교 약학대학 신주영 교수 연구팀(공동 1저자 최아형 박사, 이혜성 연구교수, 공저자 정한얼 박사)은 국내 산모ㆍ신생아 연계 보건의료 빅데이터를 활용해 산모 및 신생아에서의 항생제 사용과 어린이의 신경발달장애 발생 간의 관련성을 구명한 연구 결과를 지난 22일 세계적인 학술지 ’British Medical Journal(BMJ, (Impact Factor=107.7)’에 게재했다고 28일 밝혔다.

EHJ: 전자담배

최기홍 삼성서울병원 순환기내과 교수(사진)는 이 같은 내용이 담긴 논문 ’경피적 관상동맥 중재술을 받은 흡연자들의 전자담배 전환 예후: 한국 전국 연구’를 지난해 10월 유럽심장저널에 게재했다. 최 교수는 국민건강보험 데이터를 활용해 흡연 경험이 있는 1만7000명에 대해 조사했다. 연구팀은 관상동맥 스텐트 시술을 받은 환자를 △계속 일반 담배를 피운 그룹 △전자담배로 전환한 그룹 △완전히 금연한 그룹 등으로 나눠 예후를 면밀히 분석했다.

청구자료 특징

명세서데이터(20): 환자(ID) 병원 방문(Key) 당 1행

날짜, 진단명, 보험청구비, 입원여부 등 기본 정보

검사/처치/원내처방(30): 방문당 여러 행(동일 Key가 여러 행)

날짜, 검사/처치/처방명, 기간

원외처방(60 or 53): 방문당 여러 행(동일 Key가 여러 행)

날짜, 처방명, 기간

검진(g1e, 공단만): 1/2년마다 수행하는 건강검진

기본 검진항목, 특화검진(암, 폐암스크리닝, 영유아, 생애최초 등)

그 외: 소득(건강보험 10분위), 지역, 요양기관

청구자료 분석

폐쇄된 서버(인터넷 안됨)

R 패키지 설치도 마음대로 안됨
분석결과를 반출신청해야함: 엑셀, PPT 등으로 만들어야 함

분석SW

SAS(기본), R, Python(공단 최근)

SAS

SAS: 안정적으로 실행됨, 그 뿐

proc sql 로 sql문을 그대로 쓸 수 있음
RAM < HDD: 중간결과를 계속 저장해가면서 해야함
느림, 그렇지만 무조건 실행은 됨
통계 실행할 순 있지만, 반출파일로 정리는 어떻게?
유료: 개인적으로 쓸순 없다.

R 추천

처음 데이터 읽기 힘들다, 이후부턴 최고

SAS파일은 R에서 매우 느리게 읽힘, csv/fst 로 변환해야(최근 공단은 txt로 제공)
RAM > HDD: 유연하고 한번에 데이터 매니지먼트 가능
RAM이라 빠르지만, 서버터질 가능성
최신 통계방법론 이용, 분석결과를 테이블/PPT로 저장하기 편함
무료

data.table

기본 read/write 함수보다 30배이상 빠름
Group by 연산을 빠르게 수행
Merge, wide -> long -> wide 변환에 특화

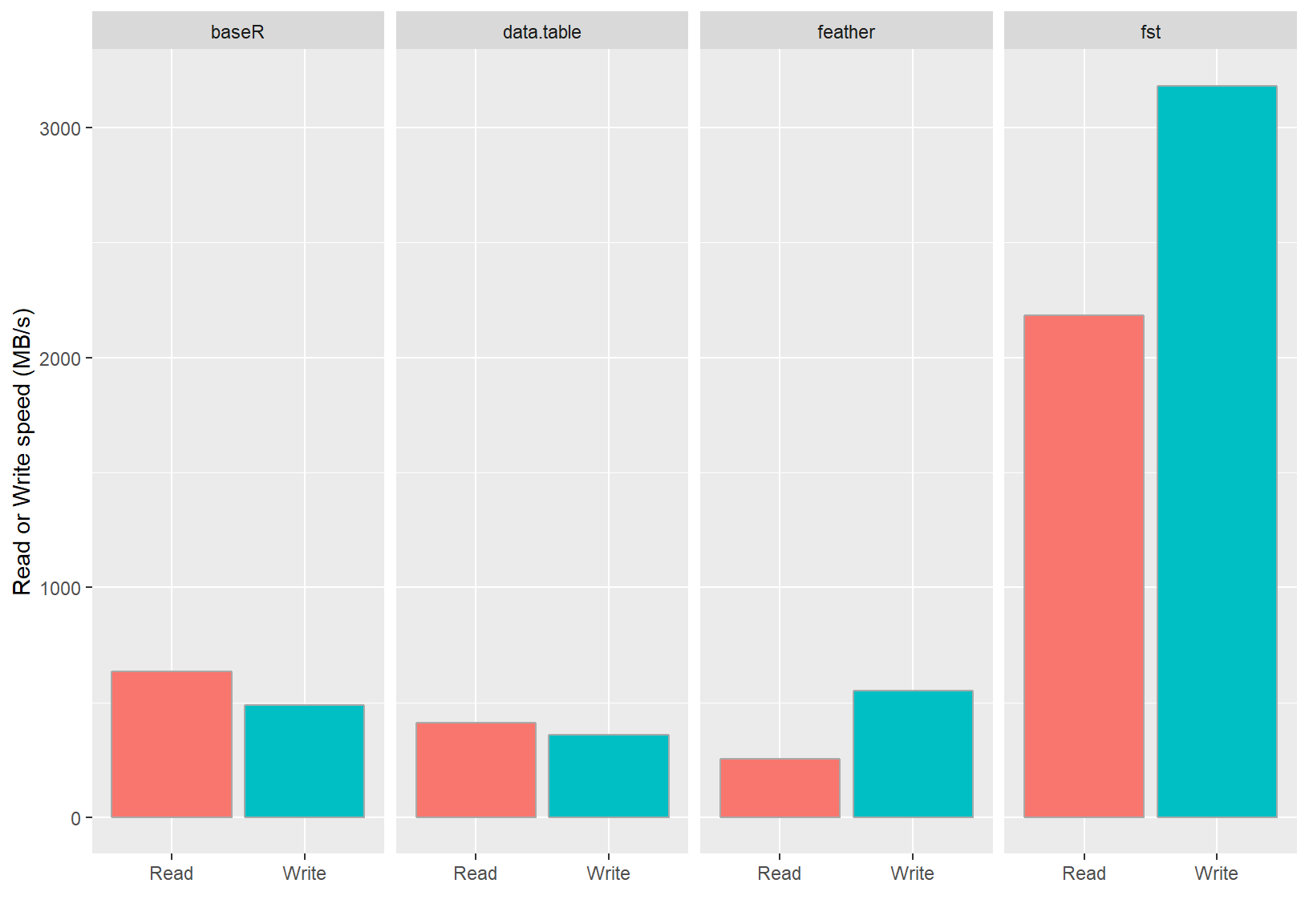
fst

R에서만 읽을 수 있는 fst 확장자 지원

data.table 보다 더 빠름
data.table 호환

공단/심평원에선 제대로 설치 못할 가능성

`%>%`: magrittr

기존 코딩: Step마다 실행

b <- subset(a, Sex == "M")
model <- glm(DM ~ Age + Weight + BMI, data = b, family = binomial)
summ.model <- summary(model)
summ.model$coefficients

%>%: 의식의 흐름대로 한번에 실행

a %>% 
  subset(Sex == "M") %>% 
  glm(DM ~ Age + Weight + BMI, data = ., family = binomial) %>% 
  summary %>% 
  .$coefficients

data.table 과 연계 추천

Multicore

parallel::mclapply : 서버에서만

다른 약물들/질병들에 대해 동일조건으로 과거력 변수 생성
다른 Outcome에 대해 동일한 분석을 반복수행(Cox, Logistic)

너무 많은 코어쓰면 공단/심평원에서 전화올 수 있음

info.cci <- parallel::mclapply(names(code.cci), function(x){
  data.asd[, MDCARE_STRT_DT := Indexdate]
  dt <- m40[like(MCEX_SICK_SYM, paste(code.cci[[x]], collapse = "|"))][, MDCARE_STRT_DT := as.Date(as.character(MDCARE_STRT_DT), format = "%Y%m%d")][, .(RN_INDI, MDCARE_STRT_DT, Incidate = MDCARE_STRT_DT)]  
  dt[, .SD[1], keyby = c("RN_INDI", "MDCARE_STRT_DT")][data.asd, on = c("RN_INDI", "MDCARE_STRT_DT"), roll = 365][, ev := as.integer(!is.na(Incidate))][]$ev * cciscore[x]
}, mc.cores = 4) %>%  do.call(cbind, .) %>% cbind(rowSums(.))
colnames(info.cci) <- c(paste0("Prev_", names(code.cci)), "CCI")

통계

흔히 쓰는 통계는 Table1을 위한 통계, Logistic/Cox/Subgroup analysis

Table 1 을 변수별로 통계구하지 않고, 한번에 수행
회귀분석은 Univariate/Multivariate 동시에 보여줘야
Subgroup analysis는 forestplot으로 보여줘야

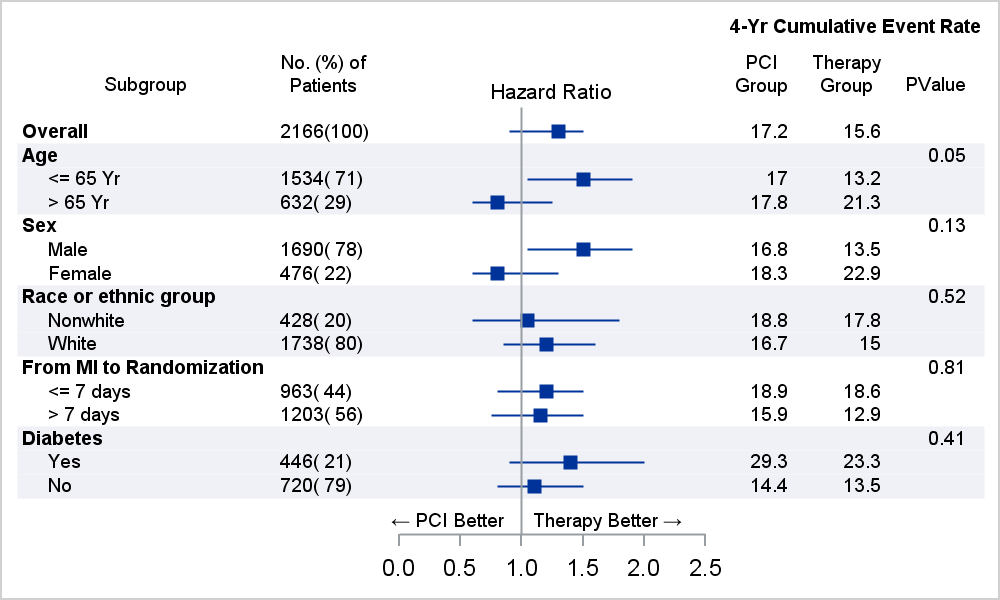
인과추론(PS/IPTW)

Baseline 맞춘다(X), RCT를 모방한다(O)

ATE(average treatment effect) vs ATT(average treatment effect on treated)
Matching은 ATT, IPTW는 ATE

2그룹 MatchIt, 3그룹 twang 패키지

Logistic regression, Nearest neighbor, caliper 이해
3그룹 matching은 가장 작은 N수에 맞춰 2번 수행
openstat.ai 에서 2그룹 matching/IPTW 지원

분석 이슈

Matching 후 pair정보 이용해야 하는가?(ex: stratified cox)
성별에 따라 매칭/IPTW 해도 되는가?

Causal inference

목표는 Causal inference, RCT like design

\(ITE = Y_{1i} - Y_{0i}\), 하늘만이..
\(ATE = E[Y_1 - Y_0]\), RCT
\(ATT = E[Y_1 - Y_0 | T=1]\), \(ATC = E[Y_1 - Y_0 | T=0]\)

PS matching

Propensity score란?

치료군 vs 대조군 연구에서, age/sex/기저질환 등의 변수를 이용하여 치료군에 속할 확률을 계산한 값
같은 PS 면 치료군에 속할 확률이 동일
같은 PS면 age/sex/기저질환 이 비슷
치료/대조군을 1/0으로 코딩하여 Logistic regression(다른 것도 가능)
치료군이 더 많다면 치료군을 0, 대조군을 1로 코딩

따라서, 치료군의 PS와 비슷한 사람을 대조군에서 뽑으면 두 그룹의 Baseline이 비슷해지겠군!

여기까지 알면 50점

RCT 관점

RCT: 어떤 사람이 두 군에 배정될 확률이 50:50

PS matching: PS가 0.7인 사람이 두 군에 배정될 확률? 50:50

PS 0.7인 사람이 치료군에 있다면, 대조군에서도 맞춰서 뽑았을 것임
여기까지 알면 90점

그럼 PS matching하면 RCT만큼 인정받을 수 있다?

No
치료군과 동일 특성을 가진 대조군이 매칭되므로, 연구집단 전체가 치료군의 특성을 가짐(예: 더 고령/ 남자가 많다 등)
ATE(average treatment effect) 가 아님, ATT(average treatment effect on the treated).

IPTW

Inverse probability of treatment weighting

매칭 안하고 모든 샘플을 씀. 단 각 사람마다 가중치가 다름
A는 1명이지만 2명처럼 간주, B는 1명이지만 10명처럼 간주
사람별 가중치를 조절하면 Baseline을 동일하게 맞출 수 있음
치료군엔 \(1/PS\), 대조군엔 \(1/(1-PS)\) 로 가중치 부여
여기까지 알면 50점

RCT 관점

PS 0.7인 사람이 각 군에 속할 확률은?

치료군 0.7, 대조군 0.3

\[0.7 \times \frac{1}{0.7} = 0.3 \times \frac{1}{0.3} = 1\]

따라서 PS 0.7인 사람이 치료군과 대조군에 동일하게 분포

그럼 IPTW는 ATE vs ATT?

ATE weight, ATT weight

ATE weight

\[ w_i \text{ for } ATE= \begin{cases} \frac{1}{p_i} & \text{if treated} \\ \frac{1}{1 - p_i} & \text{if control} \end{cases} \] 전체 샘플(Treated + Control) 의 2배를 랜덤하게 배정한 RCT

ATT weight

\[ w_i \text{ for } ATT = \begin{cases} 1 & \text{if treated} \\ \frac{p_i}{1 - p_i} & \text{if control} \end{cases} \] Treated + Treated 를 랜덤하게 배정

ATT& ATE

ATE(Average Treatment Effect): 전체 환자 집단(코호트)에서 TAVI가 수술 에 비해 효과적인가?
대조군(Surgery)와 TAVI군의 baseline을 가중치를 주어 전체 코호트(AS 환자군)와 양군을 유사하게 만들어, 전체 코호트에서 RCT를 진행하였을 때 예상되는 결과를 모사 \[ w_i = \begin{cases} \frac{1}{p_i} & \text{if treated TAVI} \\ \frac{1}{1 - p_i} & \text{if (Surgery)} \end{cases} \]

TAVI vs Surgery: Example data

ATT& ATE

name	age	TAVI	Survival	Propensity_score	ATE	ATT
빈센조	35	1	1	0.1718567	5.818801	1.0000000
루카스	48	0	1	0.3163092	1.462649	0.4626495
제이슨	50	0	1	0.3435664	1.523383	0.5233834
토마스	53	1	0	0.3864109	2.587919	1.0000000
리오넬	55	0	1	0.4160330	1.712426	0.7124256
카밀라	68	1	1	0.6136449	1.629607	1.0000000
아칸지	70	1	1	0.6424478	1.556547	1.0000000
에밀리	75	0	1	0.7097903	3.445784	2.4457837
노이어	80	1	0	0.7690095	1.300374	1.0000000
호날두	85	1	0	0.8192224	1.220670	1.0000000
앨리스	40	0	1	0.2202580	1.282475	0.2824754
밥	45	0	1	0.2777194	1.384504	0.3845035
찰리	52	0	0	0.3718948	1.592090	0.5920901
다니엘	60	1	0	0.4923210	2.031195	1.0000000
엘리자베스	62	1	1	0.5231400	1.911534	1.0000000
프랭크	67	0	1	0.5989249	2.493298	1.4932985
그레이스	73	1	1	0.6837417	1.462541	1.0000000
헨리	77	0	1	0.7345263	3.766852	2.7668518
이사벨	82	1	0	0.7901901	1.265518	1.0000000
제임스	88	1	0	0.8450253	1.183396	1.0000000
존	42	0	1	0.2421700	1.319557	0.3195571
마리아	49	0	1	0.3297948	1.492080	0.4920803
피터	54	1	0	0.4011317	2.492947	1.0000000
사라	59	1	0	0.4769187	2.096793	1.0000000
데이비드	61	0	1	0.5077378	2.031438	1.0314379
제니퍼	46	0	1	0.2902582	1.408963	0.4089632
케빈	51	1	1	0.3576063	2.796371	1.0000000
레베카	76	0	1	0.7223278	3.601369	2.6013690
토니	81	1	0	0.7797825	1.282409	1.0000000
엘리	83	1	0	0.8002318	1.249638	1.0000000
스티브	37	1	1	0.1901277	5.259622	1.0000000
안나	47	0	1	0.3031256	1.434979	0.4349789
마이클	51	0	1	0.3576063	1.556678	0.5566777
제시카	68	1	0	0.6136449	1.629607	1.0000000
댄	84	1	1	0.8099085	1.234707	1.0000000
소피아	59	0	1	0.4769187	1.911749	0.9117489
브라이언	62	1	1	0.5231400	1.911534	1.0000000
나탈리	78	0	1	0.7463771	3.942861	2.9428614
대니얼	84	1	0	0.8099085	1.234707	1.0000000
엘레나	89	1	0	0.8529311	1.172428	1.0000000
로버트	39	0	1	0.2098490	1.265581	0.2655808
줄리아	46	0	1	0.2902582	1.408963	0.4089632
스콧	53	0	0	0.3864109	1.629755	0.6297551
니콜	77	1	0	0.7345263	1.361422	1.0000000
앤드류	75	1	1	0.7097903	1.408867	1.0000000
케이트	54	0	1	0.4011317	1.669816	0.6698162
라이언	59	1	1	0.4769187	2.096793	1.0000000
미셸	86	0	1	0.8281768	5.819935	4.8199354
조셉	88	1	0	0.8450253	1.183396	1.0000000
엘레나	83	1	0	0.8002318	1.249638	1.0000000

ATT& ATE

Treatment, Control 그룹의 Age 비교
그룹	Treatment	Control
ATT	70	69.04
ATE	62.17	63.1
Original Cohort	70(63.72)	56.35(63.72)

IPTW win?

IPTW는 ATE니까 무조건 이걸해야겠네?

Weight 100 인 사람이 있다면?

Truncated weight

99% quantile 값 이상은 99%로 바꿈
weight 10 이상은 10으로 바꿈
Baseline 이 덜 맞춰지게 됨, ATE 훼손

분석난이도 증가

GLM, Cox에 Weight를 고려 (glm, cox weights 옵션 또는 svyglm, svycox)
Weighted Kaplan-meier from svycox (survfit weights 옵션 또는 svykm)

s1 <- svykm(Surv(time, status > 0) ~ sex, design = dpbc)
jskm::svyjskm(s1, pval = T, table = T, design = dpbc)

log-rank test(X), survey rank test(O, survey::svyranktest)

또는 IPWsurvival::adjusted.LR 이용(SAS 디폴트)

`MatchIt`

2그룹 PS/IPTW에서 가장 많이 쓰는 패키지

library(MatchIt)
data("lalonde", package = "MatchIt")

table(lalonde$treat)


  0   1 
429 185

#1:1 NN matching w/ replacement on a logistic regression PS
m.out <- matchit(treat ~ age + educ + race + married + 
                   nodegree + re74 + re75, data = lalonde, distance = "glm", method = "nearest", ratio = 1, caliper = NULL)
m.out

A matchit object
 - method: 1:1 nearest neighbor matching without replacement
 - distance: Propensity score
             - estimated with logistic regression
 - number of obs.: 614 (original), 370 (matched)
 - target estimand: ATT
 - covariates: age, educ, race, married, nodegree, re74, re75

distance: glm(로지스틱) 이 기본, 다른 ML모델도 가능
method: nearest 충분, ratio: 1:N 매칭
caliper: 매칭이 잘 안될때(ex: Treat/Control 숫자가 비슷할 때)

Matching data

mdata <- match.data(m.out)
rmarkdown::paged_table(mdata[order(mdata$subclass), c("treat", "distance", "subclass")])

Matching 결과 확인

summary(m.out)


Call:
matchit(formula = treat ~ age + educ + race + married + nodegree + 
    re74 + re75, data = lalonde, method = "nearest", distance = "glm", 
    caliper = NULL, ratio = 1)

Summary of Balance for All Data:
           Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance          0.5774        0.1822          1.7941     0.9211    0.3774
age              25.8162       28.0303         -0.3094     0.4400    0.0813
educ             10.3459       10.2354          0.0550     0.4959    0.0347
raceblack         0.8432        0.2028          1.7615          .    0.6404
racehispan        0.0595        0.1422         -0.3498          .    0.0827
racewhite         0.0973        0.6550         -1.8819          .    0.5577
married           0.1892        0.5128         -0.8263          .    0.3236
nodegree          0.7081        0.5967          0.2450          .    0.1114
re74           2095.5737     5619.2365         -0.7211     0.5181    0.2248
re75           1532.0553     2466.4844         -0.2903     0.9563    0.1342
           eCDF Max
distance     0.6444
age          0.1577
educ         0.1114
raceblack    0.6404
racehispan   0.0827
racewhite    0.5577
married      0.3236
nodegree     0.1114
re74         0.4470
re75         0.2876

Summary of Balance for Matched Data:
           Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance          0.5774        0.3629          0.9739     0.7566    0.1321
age              25.8162       25.3027          0.0718     0.4568    0.0847
educ             10.3459       10.6054         -0.1290     0.5721    0.0239
raceblack         0.8432        0.4703          1.0259          .    0.3730
racehispan        0.0595        0.2162         -0.6629          .    0.1568
racewhite         0.0973        0.3135         -0.7296          .    0.2162
married           0.1892        0.2108         -0.0552          .    0.0216
nodegree          0.7081        0.6378          0.1546          .    0.0703
re74           2095.5737     2342.1076         -0.0505     1.3289    0.0469
re75           1532.0553     1614.7451         -0.0257     1.4956    0.0452
           eCDF Max Std. Pair Dist.
distance     0.4216          0.9740
age          0.2541          1.3938
educ         0.0757          1.2474
raceblack    0.3730          1.0259
racehispan   0.1568          1.0743
racewhite    0.2162          0.8390
married      0.0216          0.8281
nodegree     0.0703          1.0106
re74         0.2757          0.7965
re75         0.2054          0.7381

Sample Sizes:
          Control Treated
All           429     185
Matched       185     185
Unmatched     244       0
Discarded       0       0

`jstable::CreateTableOneJS`

jstable::CreateTableOneJS(vars = names(m.out$X), strata = "treat", data = lalonde, smd = T)$table %>% kable

	level	0	1	p	SMD	sig
n		429	185			NA
age		28.03 ± 10.79	25.82 ± 7.16	0.003	0.242	**
educ		10.24 ± 2.86	10.35 ± 2.01	0.585	0.045
race (%)	black	87 (20.3)	156 (84.3)	<0.001	1.701	**
	hispan	61 (14.2)	11 ( 5.9)			NA
	white	281 (65.5)	18 ( 9.7)			NA
married		0.51 ± 0.50	0.19 ± 0.39	<0.001	0.719	**
nodegree		0.60 ± 0.49	0.71 ± 0.46	0.007	0.235	**
re74		5619.24 ± 6788.75	2095.57 ± 4886.62	<0.001	0.596	**
re75		2466.48 ± 3292.00	1532.06 ± 3219.25	0.001	0.287	**

Mathing data

jstable::CreateTableOneJS(vars = names(m.out$X), strata = "treat", data = mdata, smd = T)$table %>% kable

	level	0	1	p	SMD	sig
n		185	185			NA
age		25.30 ± 10.59	25.82 ± 7.16	0.585	0.057
educ		10.61 ± 2.66	10.35 ± 2.01	0.290	0.110
race (%)	black	87 (47.0)	156 (84.3)	<0.001	0.855	**
	hispan	40 (21.6)	11 ( 5.9)			NA
	white	58 (31.4)	18 ( 9.7)			NA
married		0.21 ± 0.41	0.19 ± 0.39	0.604	0.054
nodegree		0.64 ± 0.48	0.71 ± 0.46	0.151	0.150
re74		2342.11 ± 4238.98	2095.57 ± 4886.62	0.605	0.054
re75		1614.75 ± 2632.35	1532.06 ± 3219.25	0.787	0.028

Caliper

m.out.caliper <- matchit(treat ~ age + educ + race + married + 
                   nodegree + re74 + re75, data = lalonde, method = "nearest", ratio = 1, caliper = 0.1)
jstable::CreateTableOneJS(vars = names(m.out$X), strata = "treat", data = match.data(m.out.caliper), smd = T)$table %>% kable

	level	0	1	p	SMD	sig
n		111	111			NA
age		26.14 ± 10.88	25.95 ± 6.58	0.870	0.022
educ		10.49 ± 2.66	10.49 ± 2.04	1.000	<0.001
race (%)	black	80 (72.1)	82 (73.9)	0.954	0.041
	hispan	12 (10.8)	11 ( 9.9)			NA
	white	19 (17.1)	18 (16.2)			NA
married		0.24 ± 0.43	0.21 ± 0.41	0.523	0.086
nodegree		0.61 ± 0.49	0.65 ± 0.48	0.580	0.074
re74		2408.56 ± 4436.77	2667.11 ± 5732.76	0.707	0.050
re75		1800.87 ± 2917.71	1811.30 ± 3699.16	0.981	0.003

IPTW: `svyCreateTableOneJS`

library(survey)
lalonde$wt <- ifelse(lalonde$treat == 1, 1/m.out$distance, 1/(1 - m.out$distance))
design.lalonde <- svydesign(ids=~1, strata=NULL, weights=~wt, data = lalonde)
jstable::svyCreateTableOneJS(vars = names(m.out$X), strata = "treat", data = design.lalonde, smd = T)$table %>% kable

	level	0	1	p	SMD	sig
n		429.00	185.00			NA
age		27.10 ± 10.80	25.57 ± 6.53	0.088	0.172
educ		10.29 ± 2.74	10.61 ± 2.05	0.303	0.132
race (%)	black	87.0 (39.8)	156.0 (44.8)	0.695	0.112
	hispan	61.0 (11.7)	11.0 (12.2)			NA
	white	281.0 (48.5)	18.0 (43.0)			NA
married		0.41 ± 0.49	0.31 ± 0.47	0.228	0.197
nodegree		0.62 ± 0.48	0.57 ± 0.50	0.458	0.112
re74		4552.74 ± 6337.09	2932.18 ± 5709.42	0.040	0.269	**
re75		2172.04 ± 3160.14	1658.07 ± 3072.89	0.136	0.165

openstat.ai

3그룹 A vs B vs C

Matching: N수 제일 작은 그룹(A) 에 맞춰 여러번 매칭

MatchIt 그대로 쓸 수 있는건 장점
\(ATT\)도 아닌 \(ATT_{A}\)?

IPTW: twang::mnps

시간이 오래걸림: 공단데이터에서 24시간 걸릴수도
\(ATE\) 가능, 더 추천

Issue 1: Matching 후 pair정보 이용

Matching 후 stratified cox를 해야하는가? Yes or No

cox1 <- coxph(Surv(time, status) ~ treat, data = mdata)

cox2 <- coxph(Surv(time, status) ~ treat + strata(subclass), data = mdata)

Pair 마다 baseline hazard가 다르다는 가정

RCT 재현 관점: 필요없음(pair정보 없음)
매칭이 너무 잘 되어서 pair정보가 확실하다면?
Pair 들끼리 뭔가 다르다면?
OMOP-CDM ATLAS에서는 strata 사용하는게 Default.

번외: baseline hazard 보정방법

예) 다기관 RCT에서 hospital, stratified random

cox1 <- coxph(Surv(time, status) ~ treat + strata(hospital), data = mdata)

cox2 <- coxph(Surv(time, status) ~ treat + hospital, data = mdata)

cox3 <- coxme::coxme(Surv(time, status) ~ treat + (1|hospital), data = mdata)

cox4 <- coxph(Surv(time, status) ~ treat, data = mdata, cluster = hospital)

+ hospital 도 가능, but 각 병원의 계수를 굳이 구할필요가?
coxme: mixed model의 Random effect, strata와 비슷한 의미
cluster = hospital: 같은 hospital 간에 상관관계가 있음을 보정하므로 strata와 비슷한 의미일 것 같지만, baseline hazard 이 다르다는 가정이 아님. cluster 옵션 전후 HR은 변하지 않음, SE만 변화.

Issue 2: Sex를 그룹변수로 Matching 가능?

Sex가 RCT 가능한가?

불가능 vs 하늘(?) 이 준 랜덤

Matching: \(ATT\)

남자 vs 남자같은 여자, 여자 vs 여자같은 남자

IPTW: \(ATE\) 니까 OK?

전체 연구대상자(남자 + 여자) 를 남/여 1:1로 랜덤배정했다는 뜻

자체 개발 R package

CRAN(총 20만회 다운로드)

jskm: 생존분석 그림
jstable: 분석결과를 보고서/논문용 테이블로
jsmodule: Shiny module & 로컬에서 실행하는 분석웹

일본 블로그 리뷰

Landmark, Competing risk analysis support

## Gaussian
glm_gaussian <- glm(mpg~cyl + disp, data = mtcars)
glmshow.display(glm_gaussian, decimal = 2)

$first.line
[1] "Linear regression predicting mpg\n"

$table
     crude coeff.(95%CI)   crude P value adj. coeff.(95%CI)    adj. P value
cyl  "-2.88 (-3.51,-2.24)" "< 0.001"     "-1.59 (-2.98,-0.19)" "0.034"
disp "-0.04 (-0.05,-0.03)" "< 0.001"     "-0.02 (-0.04,0)"     "0.054"

$last.lines
[1] "No. of observations = 32\nR-squared = 0.7596\nAIC value = 167.1456\n\n"

## Binomial
glm_binomial <- glm(vs~cyl + disp, data = mtcars, family = binomial)
glmshow.display(glm_binomial, decimal = 2)

$first.line
[1] "Logistic regression predicting vs\n"
 
$table
     crude OR.(95%CI)   crude P value adj. OR.(95%CI)    adj. P value
cyl  "0.2 (0.08,0.56)"  "0.002"       "0.15 (0.02,1.02)" "0.053"     
disp "0.98 (0.97,0.99)" "0.002"       "1 (0.98,1.03)"    "0.715"     

$last.lines
[1] "No. of observations = 32\nAIC value = 23.8304\n\n"

Subgroup analysis

TableSubgroupMultiGLM(status ~ sex, var_subgroups = c("kk", "kk1"), data = lung, family = "binomial")

    Variable Count Percent           OR Lower Upper P value P for interaction
sex2  Overall   228     100         3.01  1.65  5.47  <0.001              <NA>
1          kk  <NA>    <NA>         <NA>  <NA>  <NA>    <NA>             0.476
2           0    38    16.9            7   0.7 70.03   0.098              <NA>
3           1   187    83.1         2.94  1.55  5.57   0.001              <NA>
4         kk1  <NA>    <NA>         <NA>  <NA>  <NA>    <NA>             0.984
5           0     8     3.6 314366015.19     0   Inf   0.997              <NA>
6           1   217    96.4         2.85  1.55  5.25   0.001              <NA>

TableSubgroupMultiCox(Surv(time, status) ~ sex, var_subgroups = c("kk", "kk1"), data = lung)

    Variable Count Percent Point Estimate Lower Upper sex=1 sex=2 P value P for interaction
sex  Overall   228     100           1.91  1.14   3.2   100   100   0.014              <NA>
1       <NA>  <NA>    <NA>           <NA>  <NA>  <NA>  <NA>  <NA>    <NA>              <NA>
2         kk  <NA>    <NA>           <NA>  <NA>  <NA>  <NA>  <NA>    <NA>             0.525
3          0    38    16.9           2.88  0.31 26.49    10   100    0.35              <NA>
4          1   187    83.1           1.84  1.08  3.14   100   100   0.026              <NA>
5       <NA>  <NA>    <NA>           <NA>  <NA>  <NA>  <NA>  <NA>    <NA>              <NA>
6        kk1  <NA>    <NA>           <NA>  <NA>  <NA>  <NA>  <NA>    <NA>             0.997
7          0     8     3.6           <NA>  <NA>  <NA>     0   100    <NA>              <NA>
8          1   217    96.4           1.88  1.12  3.17   100   100   0.018              <NA>

중국 영상/블로그 리뷰

1-2줄의 코드만으로 분석웹을 만들 수 있도록 각 분석기능을 모듈화

무료 통계웹

흔한 분석기능들을 무료로 분석할 수 있는 openstat.ai 런칭
jskm/jstable/jsmodule 분석모듈 적용

openstat.ai: free

맞춤형 분석웹은 유료제작

오픈소스기여: 인턴십

정기적 선발

인턴의 오픈소스 패키지개발 참여

교육

성균관대학교 바이오헬스규제과학과 겸임교수 강의

https://github.com/jinseob2kim/r-skku-biohrs
R활용 의료데이터분석, 강의록과 강의영상 모두 공개

분석결과 공유: 연구자와의 소통

SPSS, SAS, R 결과를 그냥 보내줄 수 없음.

그럼 엑셀/Word 테이블을 직접?
그림 수정해달라고 한다면?

몇번만 왔다갔다하면 서로 지침

Solution 1: R로 직접 테이블, PPT 작성

R에서 테이블형태로 만들고, 이것들을 모아 하나의 엑셀로 저장

openxlsx::write.xlsx(list(Baseline = tb1old, Baseline_add = tb1add, OR = res.OR), "new.xlsx", rowNames = T)

Soultion 2: Flextable로 Word생성

## Continuous Exposure, Add Phase/Remove ICU day to covariates
tb2.add <- lapply(c("Energy", "Protein"), function(v){
  covs <- c("Phase", "age", "sex", "baseline_SOFA", "malnutrition")
  form <- paste0("death_180days", "~", v, "+", paste(covs, collapse = "+"), "+ (1|No)")
  model <- glmer(as.formula(form), data = along, family = binomial, nAGQ = 0)
  tbl_regression(model, exponentiate = T, estimate_fun = function(x) style_number(x, digits = 2),
                 pvalue_fun = function(x) style_number(x, digits = 3)) %>% bold_p(t = 0.05) %>% bold_labels() %>% 
    as_flex_table()
})

save_as_docx(Energy = tb2.add[[1]], Protein = tb2.add[[2]], path = "table2_add.docx")

Figure as PPT

편집가능한 벡터그래픽으로 제공

library(rvg);library(officer)
doc <- read_pptx() %>% 
       add_slide() %>% 
       ph_with(dml(ggobj = gg_plot),
   location = ph_location_type(type = "body"))
print(doc, target = "reports/rvg.pptx")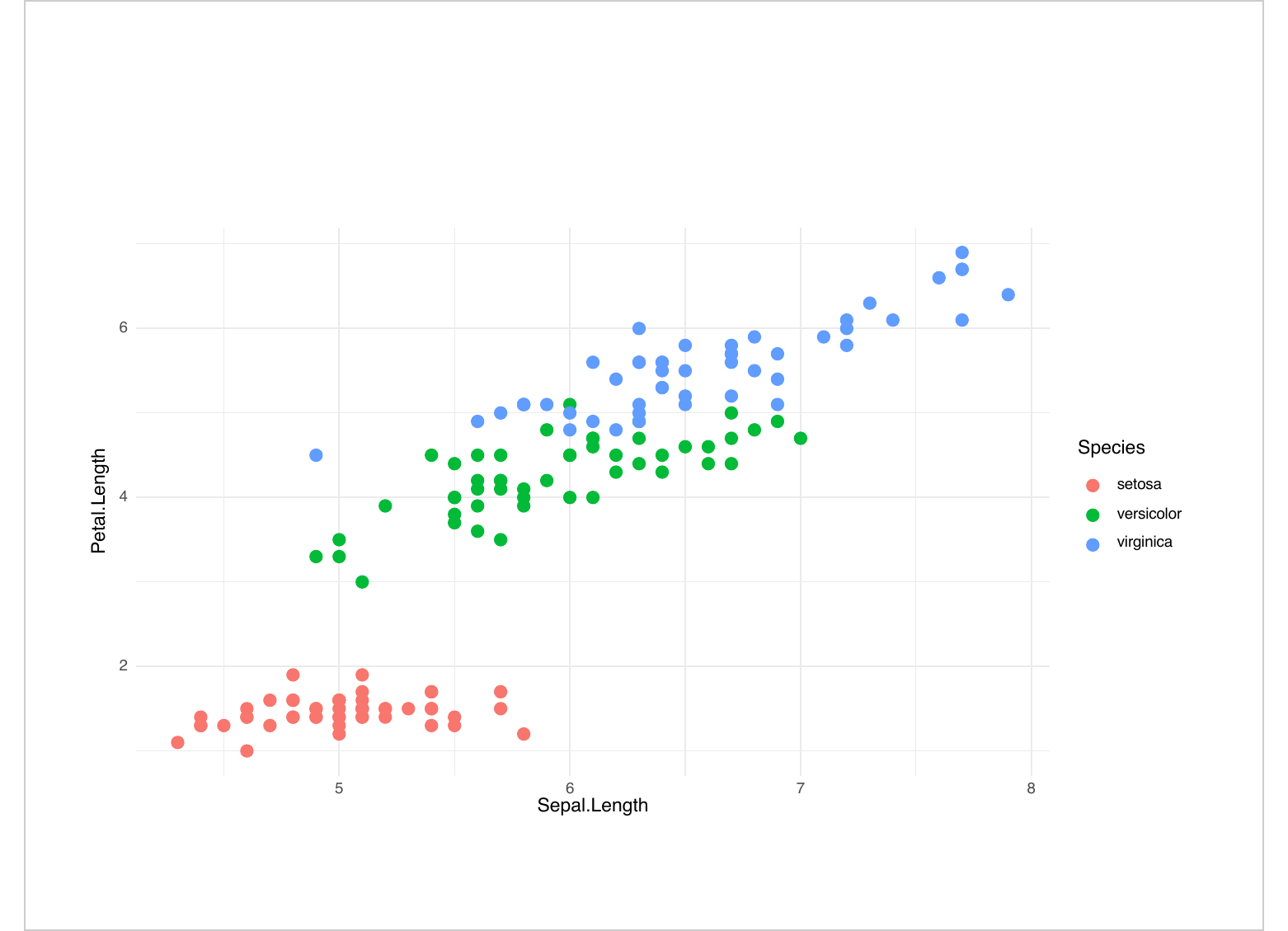

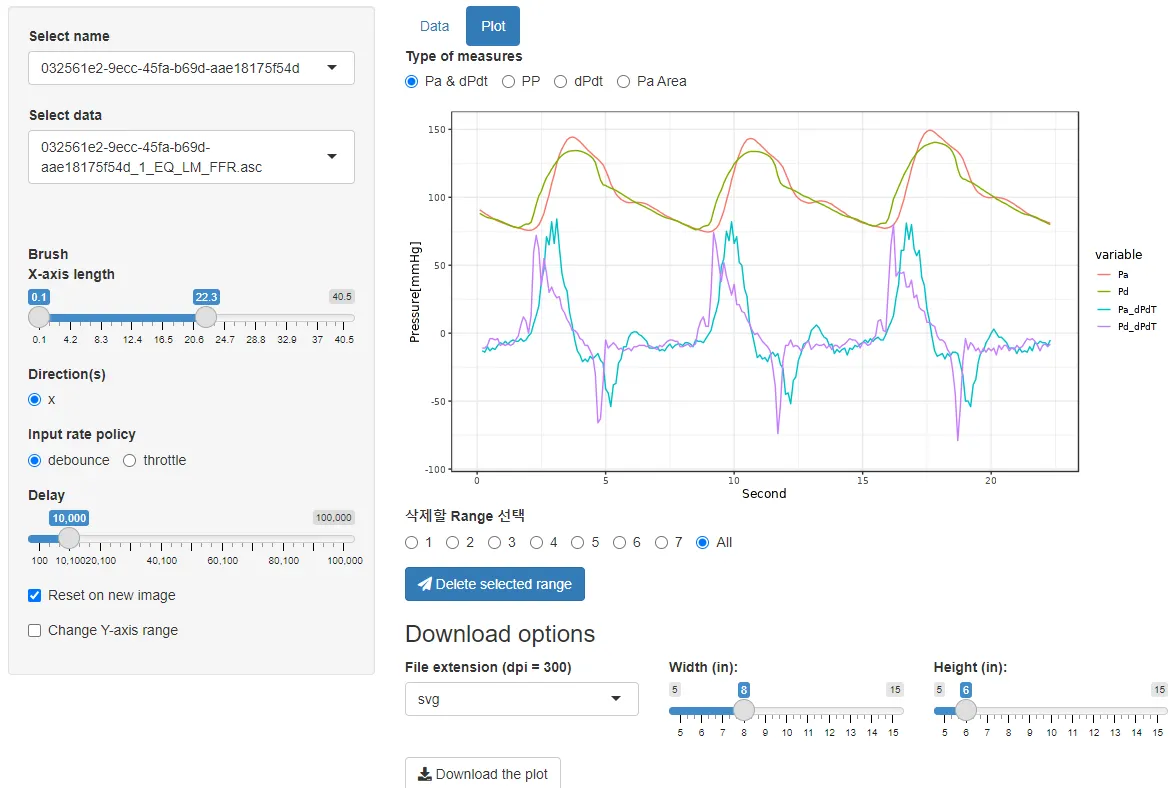
웹 애플리케이션: Shiny

분석옵션을 조절하고 그 결과를 다운받을 수 있도록 제작

Executive summary

병원데이터: (1) 연구위해 정리된 (2) 연구위해 정리해야 할

정리된: 개인연구자 엑셀, 레지스트리, RCT
정리 필요: CDW, CDM, 공단/심평원

데이터 정리: R(CPU < RAM)

data.table: 빠른 읽기/쓰기, 환자ID 별 작업, melt/dcast
fst: fst 확장자 통한 가장 빠른 읽기/쓰기
%>% operater: 의식의 흐름대로 코드짜기, parallel::mclapply: 멀티코어

많이 쓰는 통계: logistic, survival, subgroup analysis, 인과추론(PS/IPTW)

자체개발한 jstable, jskm, jsmodule R 패키지, 무료웹 https://openstat.ai

분석결과 공유: 엑셀, PPT, 워드, 웹 애플리케이션: officer/rvg/flextable/shiny

빅데이터 활용 제약바이오연구 소개

자기소개

Executive summary

정리된 데이터

정리 필요한 데이터: Real World Data(RWD)

CDW

CDM

Why CDM(2)

Why CDM(3)

OMOP CDM V6

Standardized Vocabulary 예

국내 참여 병원

HIRA CDM

R first

분석코드, 결과도 R패키지

ATLAS

데이터 소스

컨셉세트

코호트 정의

분석

R패키지 다운

Feedernet 이용

단계

Textbook

연구지원경험: 심평원 Covid-19 데이터

강동성심병원

공단표본코호트 V1

공단표본코호트 V1(2)

공단표본코호트 V1(3)

Feedernet 다기관메타

Feedernet 다기관메타(2)

Feedernet 다기관메타(3)

CDM summary

공단, 심평원

BMJ: 산모 자녀 매칭

EHJ: 전자담배

청구자료 특징

청구자료 분석

SAS

R 추천

data.table

fst

%>%: magrittr

Multicore

통계

인과추론(PS/IPTW)

Causal inference

PS matching

RCT 관점

IPTW

RCT 관점

ATE weight, ATT weight

ATT& ATE

TAVI vs Surgery: Example data

ATT& ATE

ATT& ATE

IPTW win?

MatchIt

Matching data

Matching 결과 확인

jstable::CreateTableOneJS

Mathing data

Caliper

IPTW: svyCreateTableOneJS

openstat.ai

3그룹 A vs B vs C

Issue 1: Matching 후 pair정보 이용

번외: baseline hazard 보정방법

Issue 2: Sex를 그룹변수로 Matching 가능?

자체 개발 R package

일본 블로그 리뷰

Subgroup analysis

중국 영상/블로그 리뷰

무료 통계웹

오픈소스기여: 인턴십

교육

분석결과 공유: 연구자와의 소통

Solution 1: R로 직접 테이블, PPT 작성

Soultion 2: Flextable로 Word생성

Figure as PPT

`%>%`: magrittr

`MatchIt`

`jstable::CreateTableOneJS`

IPTW: `svyCreateTableOneJS`