시작하기 전에

본 강의록은 GAM 이론은 생략한다. 이론은 https://www.slideshare.net/secondmath/generalized-additive-model 을 참고하기 바란다.

Example data: Korea airpolution

#install.packages("HEAT")
library(HEAT)
data(mort)
head(mort)
ccode cname yy mm dd date nonacc cardio respir influenza meanpm10 meanso2 meanno2 meanco maxco maxo3 meantemp maxtemp mintemp meanhumi meanpress season dow sn
11 sl 2000 1 1 2000-01-01 139 30 13 NA 72.05 5.89 38.18 11.22 12.84 21.35 5.34 9.4 2.0 64.38 1024.60 4 7 1
11 sl 2000 1 2 2000-01-02 144 34 16 NA 55.06 5.79 26.26 11.65 14.25 25.22 4.55 6.8 -0.9 74.38 1016.29 4 1 2
11 sl 2000 1 3 2000-01-03 130 41 10 NA 62.50 5.42 27.84 10.04 10.50 19.96 -2.13 0.0 -4.4 55.42 1022.95 4 2 3
11 sl 2000 1 4 2000-01-04 149 37 18 NA 105.24 9.85 43.85 15.76 18.32 7.44 0.05 3.9 -4.0 49.75 1024.99 4 3 4
11 sl 2000 1 5 2000-01-05 143 42 18 NA 76.58 5.95 39.86 13.76 14.63 9.29 2.66 4.6 0.2 82.33 1018.69 4 4 5
11 sl 2000 1 6 2000-01-06 136 38 4 NA 50.40 4.74 30.50 12.18 14.83 15.91 1.98 5.5 -4.2 78.75 1015.85 4 5 6

Descriptive(Seoul): ts class

sl = subset(mort,ccode==11)
sl.ts = ts(sl, start=c(2000,1), frequency = 365.25)
plot(sl.ts[,c("nonacc","meanpm10","meanso2","meanno2","meantemp")],main="Description")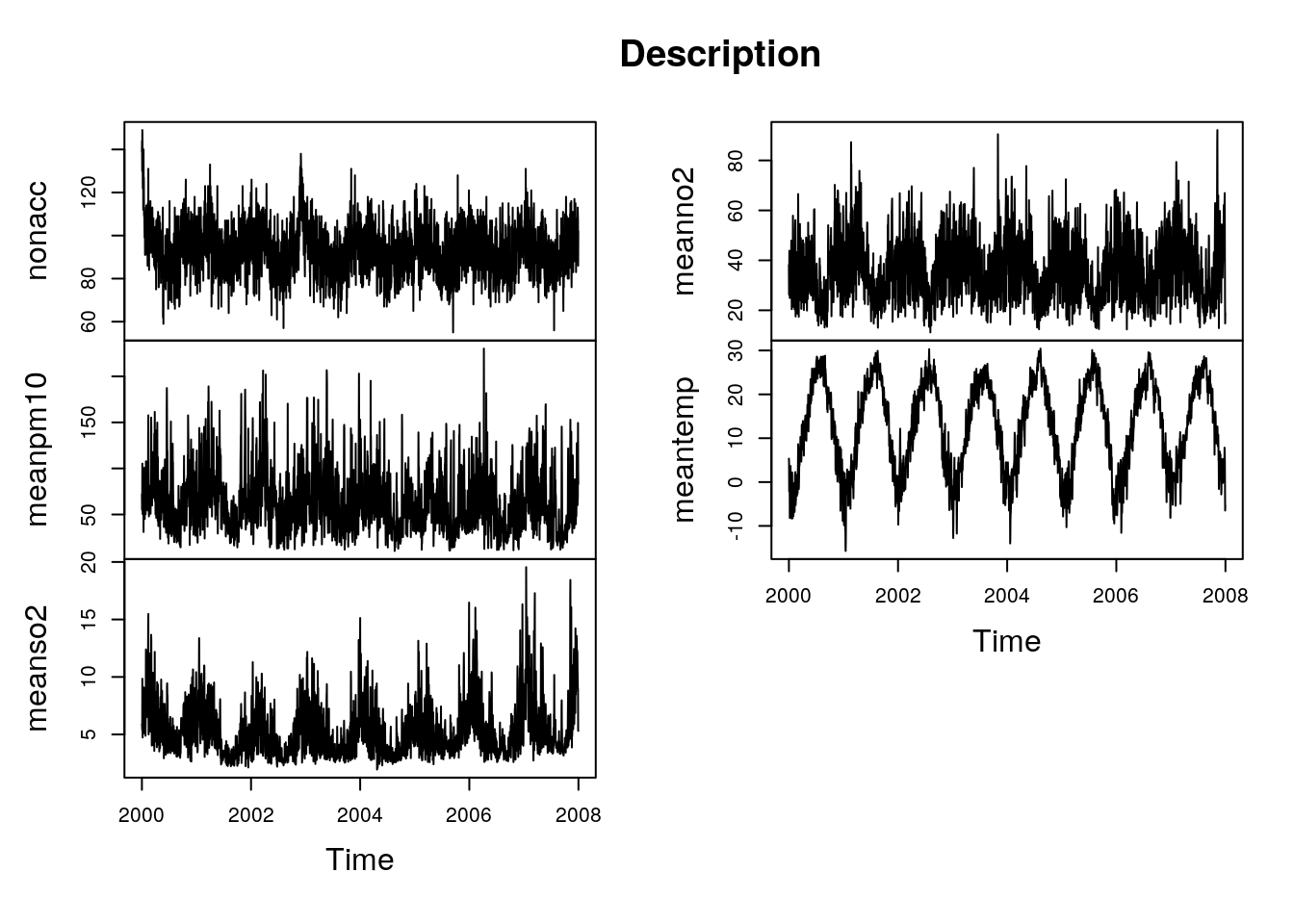

plot(decompose(sl.ts[,"nonacc"],type="multiplicative"))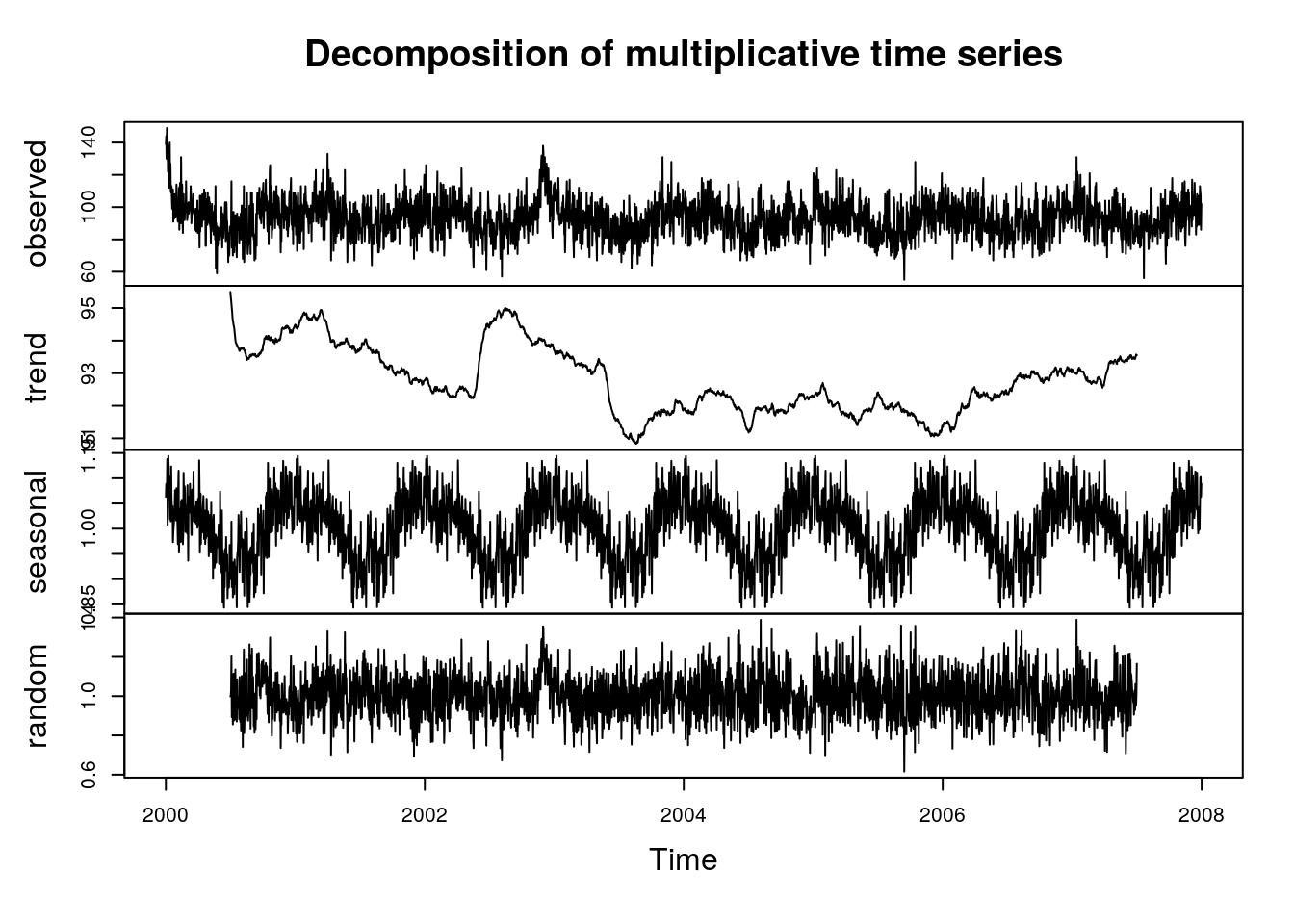

ACF: Autocorrelation Function

acf(sl$nonacc,main="Seoul: nonacc",lag.max=10)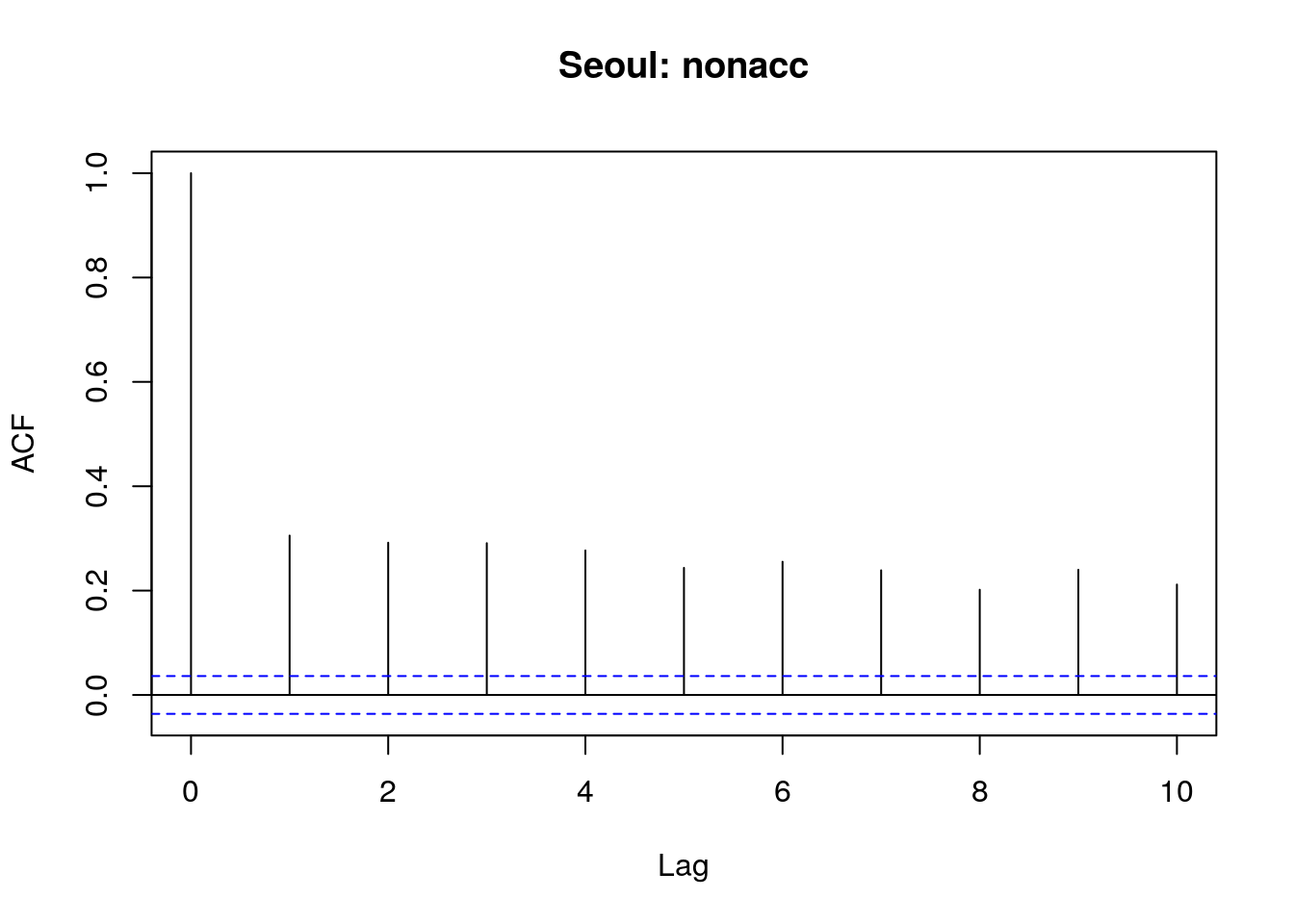

pacf(sl$nonacc,main="Seoul: nonacc",lag.max=10)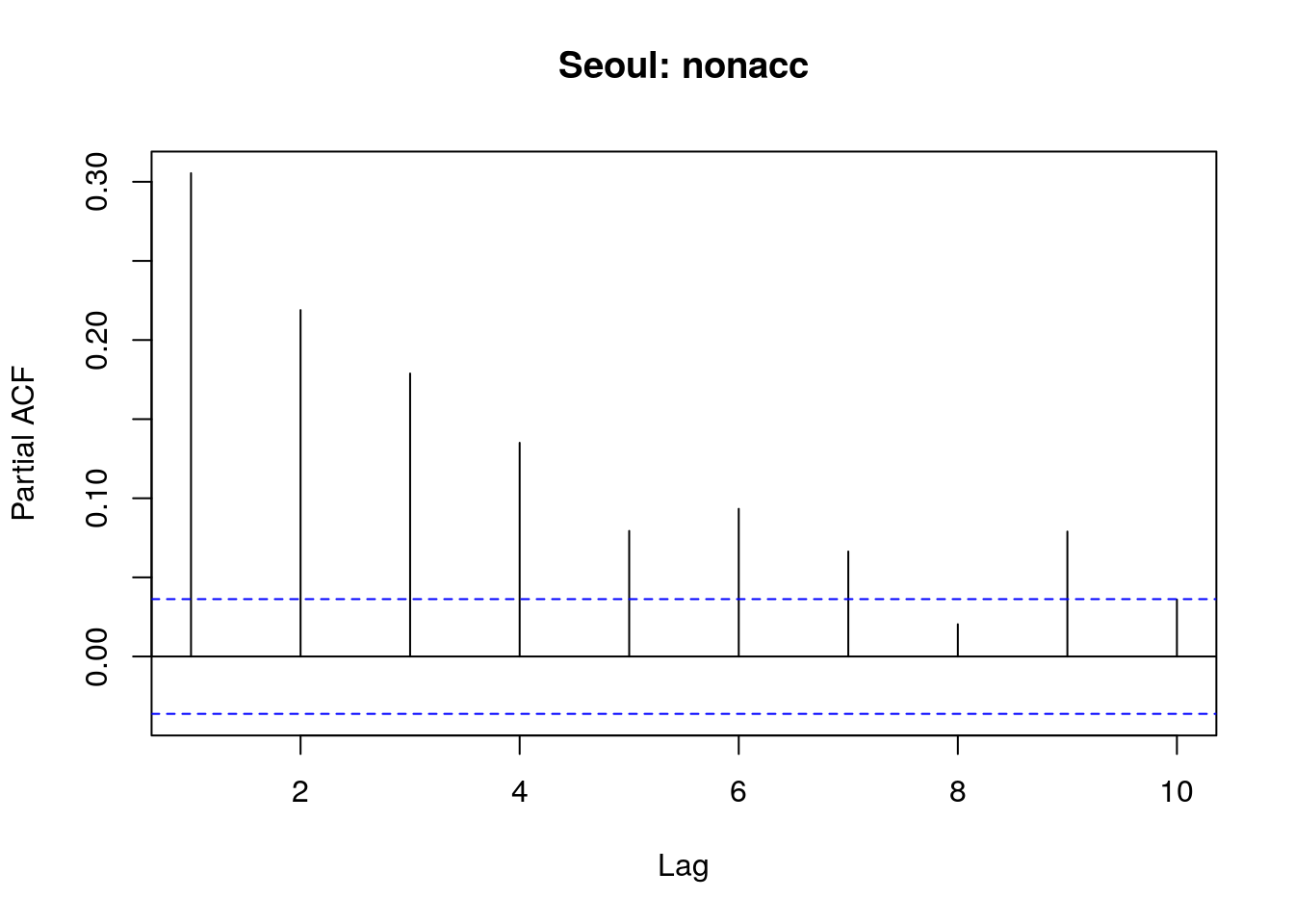

서울시 인구수: For offset

다음 자료를 참고하여 서울의 2000~2007년의 인구수 정보를 얻었다.

https://www.google.co.kr/publicdata/explore?ds=z5567oe244g0ot_&ctype=c&strail=false&bcs=d&nselm=s&met_y=population&scale_y=lin&ind_y=false&ifdim=city_proper:area:410&tunit=Y&pit=1188399600000&hl=en&dl=en&ind=false&icfg

pop_seoul=data.frame(yy=2000:2007,pop=c(9895220, 9880180, 9865190, 9850200, 9835200, 9820170, 10020120, 10025670))
pop_seoul
Population number 2000-2007: Seoul
yy pop
2000 9895220
2001 9880180
2002 9865190
2003 9850200
2004 9835200
2005 9820170
2006 10020120
2007 10025670

계절성 변수: sin, cos

sl$season1=sin(1:nrow(sl)/365.25*2*pi)
sl$season2=cos(1:nrow(sl)/365.25*2*pi)

par(mfrow=c(2,1))
plot(sl$season1,main="sin")
plot(sl$season2,main="cos")

Scatterplot

library(ggplot2)
ggplot(sl,aes(meanpm10,nonacc))+geom_point()+stat_smooth(method="loess",span=0.5)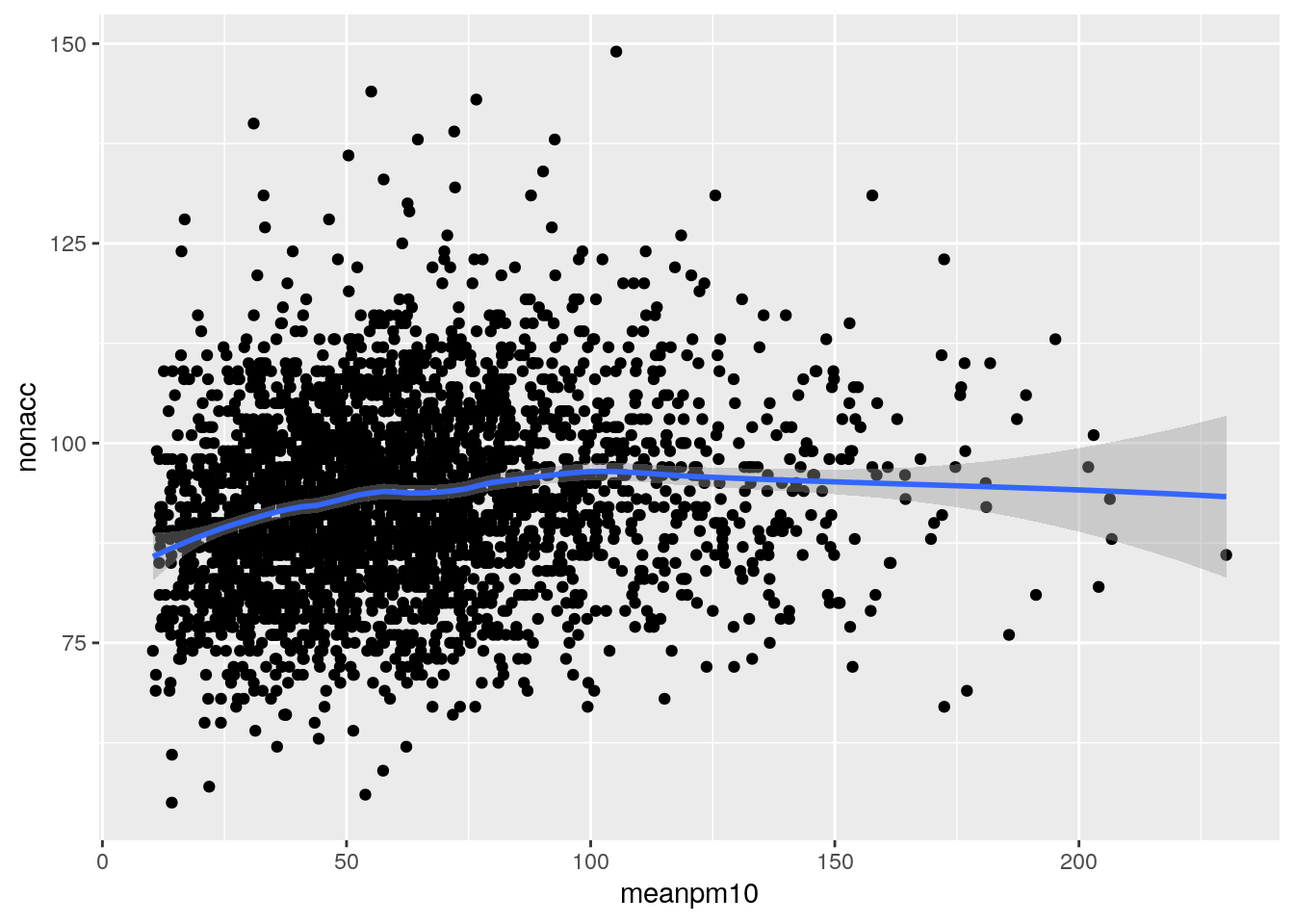

ggplot(sl,aes(meanso2,nonacc))+geom_point()+stat_smooth(method="loess",span=0.5)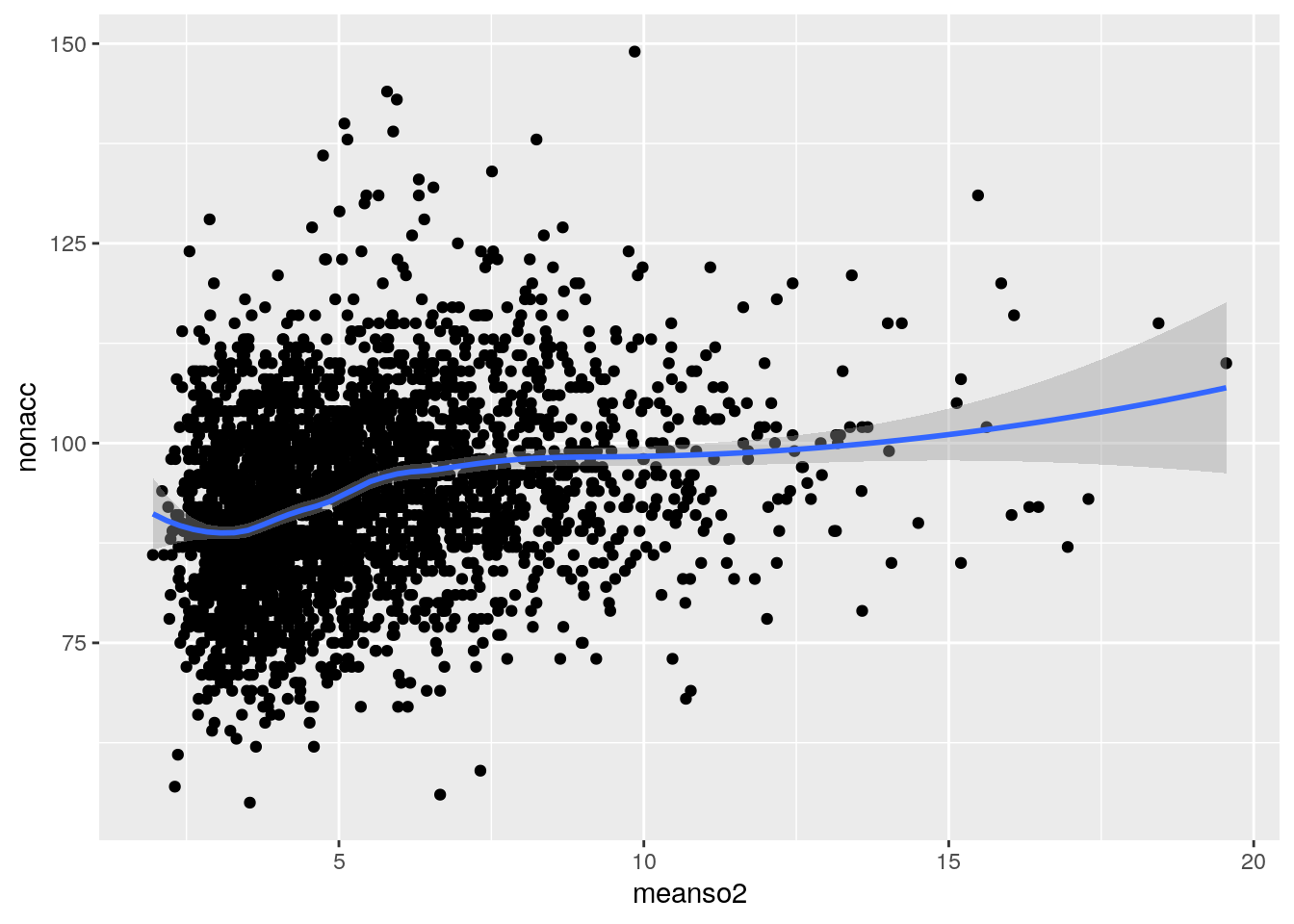

GLM

library(epiDisplay)
m1=glm(nonacc~meanpm10 + meanso2 + meanno2 + meanco + meantemp + meanhumi+ meanpress+ season1+season2, family=poisson, data=sl)

res1=idr.display(m1,crude.p.value = T)
res1
Poisson regression predicting nonacc
crude IDR(95%CI) crude P value adj. IDR(95%CI) P(Wald’s test) P(LR-test)
meanpm10 (cont. var.) 1.0006 (1.0005,1.0007) < 0.001 1 (0.9999,1.0002) 0.634 0.634
meanso2 (cont. var.) 1.01 (1.01,1.02) < 0.001 1.0005 (0.9978,1.0032) 0.735 0.735
meanno2 (cont. var.) 1.0022 (1.0019,1.0025) < 0.001 0.9995 (0.999,1.0001) 0.078 0.078
meanco (cont. var.) 1.01 (1.01,1.01) < 0.001 1.0058 (1.0037,1.0079) < 0.001 < 0.001
meantemp (cont. var.) 0.9958 (0.9955,0.9962) < 0.001 1.0037 (1.0024,1.0051) < 0.001 < 0.001
meanhumi (cont. var.) 0.9984 (0.9982,0.9987) < 0.001 0.9994 (0.999,0.9997) < 0.001 < 0.001
meanpress (cont. var.) 1.005 (1.0045,1.0055) < 0.001 1 (0.999,1.0009) 0.957 0.957
season1 (cont. var.) 1.02 (1.01,1.02) < 0.001 1.03 (1.02,1.04) < 0.001 < 0.001
season2 (cont. var.) 1.07 (1.07,1.08) < 0.001 1.11 (1.09,1.13) < 0.001 < 0.001
x
Log-likelihood = -11023.5412

No. of observations = 2921 AIC value = 22067.0825 |

Offset: Population number

sl_pop=merge(sl,pop_seoul,by="yy") 
head(sl_pop)
yy ccode cname mm dd date nonacc cardio respir influenza meanpm10 meanso2 meanno2 meanco maxco maxo3 meantemp maxtemp mintemp meanhumi meanpress season dow sn season1 season2 pop
2000 11 sl 1 1 2000-01-01 139 30 13 NA 72.05 5.89 38.18 11.22 12.84 21.35 5.34 9.4 2.0 64.38 1024.60 4 7 1 0.0172016 0.9998520 9895220
2000 11 sl 1 2 2000-01-02 144 34 16 NA 55.06 5.79 26.26 11.65 14.25 25.22 4.55 6.8 -0.9 74.38 1016.29 4 1 2 0.0343981 0.9994082 9895220
2000 11 sl 1 3 2000-01-03 130 41 10 NA 62.50 5.42 27.84 10.04 10.50 19.96 -2.13 0.0 -4.4 55.42 1022.95 4 2 3 0.0515844 0.9986686 9895220
2000 11 sl 1 4 2000-01-04 149 37 18 NA 105.24 9.85 43.85 15.76 18.32 7.44 0.05 3.9 -4.0 49.75 1024.99 4 3 4 0.0687554 0.9976335 9895220
2000 11 sl 1 5 2000-01-05 143 42 18 NA 76.58 5.95 39.86 13.76 14.63 9.29 2.66 4.6 0.2 82.33 1018.69 4 4 5 0.0859061 0.9963032 9895220
2000 11 sl 1 6 2000-01-06 136 38 4 NA 50.40 4.74 30.50 12.18 14.83 15.91 1.98 5.5 -4.2 78.75 1015.85 4 5 6 0.1030314 0.9946781 9895220 
m2=glm(nonacc~offset(log(pop))+meanpm10 + meanso2 + meanno2 + meanco + meantemp + meanhumi+ meanpress+ season1+season2, family=poisson, data=sl_pop)
res2=idr.display(m2,crude.p.value = T)
res2
Poisson regression predicting nonacc with offset = NULL : Offset as Log(pop)
crude IDR(95%CI) crude P value adj. IDR(95%CI) P(Wald’s test) P(LR-test)
meanpm10 (cont. var.) 1.0006 (1.0005,1.0007) < 0.001 1.0001 (0.9999,1.0003) 0.266 0.266
meanso2 (cont. var.) 1.01 (1.01,1.02) < 0.001 0.999 (0.9963,1.0017) 0.467 0.467
meanno2 (cont. var.) 1.0022 (1.0019,1.0025) < 0.001 0.9996 (0.9991,1.0001) 0.112 0.112
meanco (cont. var.) 1.01 (1.01,1.01) < 0.001 1.006 (1.0039,1.0081) < 0.001 < 0.001
meantemp (cont. var.) 0.9958 (0.9955,0.9962) < 0.001 1.0036 (1.0023,1.005) < 0.001 < 0.001
meanhumi (cont. var.) 0.9984 (0.9982,0.9987) < 0.001 0.9994 (0.9991,0.9997) < 0.001 < 0.001
meanpress (cont. var.) 1.005 (1.0045,1.0055) < 0.001 1 (0.9991,1.001) 0.918 0.918
season1 (cont. var.) 1.02 (1.01,1.02) < 0.001 1.03 (1.02,1.04) < 0.001 < 0.001
season2 (cont. var.) 1.07 (1.07,1.08) < 0.001 1.11 (1.08,1.13) < 0.001 < 0.001
x
Log-likelihood = -11027.097

No. of observations = 2921 AIC value = 22074.1939 |

Quasi-poisson

Overdispersion Problem: 포아송분포 가정에서는 평균=분산이 성립한다. 그러나 실제로 이런 경우는 많지 않다.

mean(sl_pop$nonacc)
## [1] 93.1564
var(sl_pop$nonacc)
## [1] 135.3774

이 때, 평균=\(\alpha\times\)분산 이 성립하는 \(\alpha\)를 추가하여 이를 해결한다. 이 결과 \(\beta\)값들은 포아송분포일 때와 동일하나 \(p\)-value가 바뀐다. 또한 모형평가하는 \(AIC\)같은 지표를 구할 수 없다.

m3=glm(nonacc~offset(log(pop))+meanpm10 + meanso2 + meanno2 + meanco + meantemp + meanhumi+ meanpress+ season1+season2, family=quasipoisson, data=sl_pop)

summary(m3)
## 
## Call:
## glm(formula = nonacc ~ offset(log(pop)) + meanpm10 + meanso2 + 
##     meanno2 + meanco + meantemp + meanhumi + meanpress + season1 + 
##     season2, family = quasipoisson, data = sl_pop)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.7976  -0.7554  -0.0389   0.6881   4.1180  
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.166e+01  5.349e-01 -21.796  < 2e-16 ***
## meanpm10     9.207e-05  9.026e-05   1.020  0.30778    
## meanso2     -1.006e-03  1.510e-03  -0.666  0.50527    
## meanno2     -4.133e-04  2.841e-04  -1.455  0.14580    
## meanco       5.966e-03  1.179e-03   5.061 4.43e-07 ***
## meantemp     3.637e-03  7.398e-04   4.917 9.29e-07 ***
## meanhumi    -6.087e-04  1.861e-04  -3.271  0.00108 ** 
## meanpress    4.896e-05  5.217e-04   0.094  0.92525    
## season1      2.572e-02  5.225e-03   4.922 9.04e-07 ***
## season2      1.001e-01  1.046e-02   9.563  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 1.190775)
## 
##     Null deviance: 4227.2  on 2920  degrees of freedom
## Residual deviance: 3458.8  on 2911  degrees of freedom
##   (1 observation deleted due to missingness)
## AIC: NA
## 
## Number of Fisher Scoring iterations: 4
summary(m2) ## 비교
## 
## Call:
## glm(formula = nonacc ~ offset(log(pop)) + meanpm10 + meanso2 + 
##     meanno2 + meanco + meantemp + meanhumi + meanpress + season1 + 
##     season2, family = poisson, data = sl_pop)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.7976  -0.7554  -0.0389   0.6881   4.1180  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -1.166e+01  4.902e-01 -23.784  < 2e-16 ***
## meanpm10     9.207e-05  8.271e-05   1.113 0.265656    
## meanso2     -1.006e-03  1.384e-03  -0.727 0.467175    
## meanno2     -4.133e-04  2.603e-04  -1.588 0.112368    
## meanco       5.966e-03  1.080e-03   5.523 3.34e-08 ***
## meantemp     3.637e-03  6.780e-04   5.365 8.09e-08 ***
## meanhumi    -6.087e-04  1.705e-04  -3.570 0.000357 ***
## meanpress    4.896e-05  4.781e-04   0.102 0.918443    
## season1      2.572e-02  4.789e-03   5.371 7.82e-08 ***
## season2      1.001e-01  9.589e-03  10.435  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 4227.2  on 2920  degrees of freedom
## Residual deviance: 3458.8  on 2911  degrees of freedom
##   (1 observation deleted due to missingness)
## AIC: 22074
## 
## Number of Fisher Scoring iterations: 4

GAM

m4=gam(nonacc~offset(log(pop))+s(meanpm10) + s(meanso2) + s(meanno2) + s(meanco) + s(meantemp) + s(meanhumi)+ s(meanpress)+ season1+season2, family=poisson, data=sl_pop)

summary(m4)$edf ## Effective Degree of Freedom
## [1] 3.665217 4.760229 2.469260 1.000158 7.366861 1.000997 3.319915
AIC(m4)         ## AIC
## [1] 22016.55
par(mfrow=c(2,4))
plot(m4)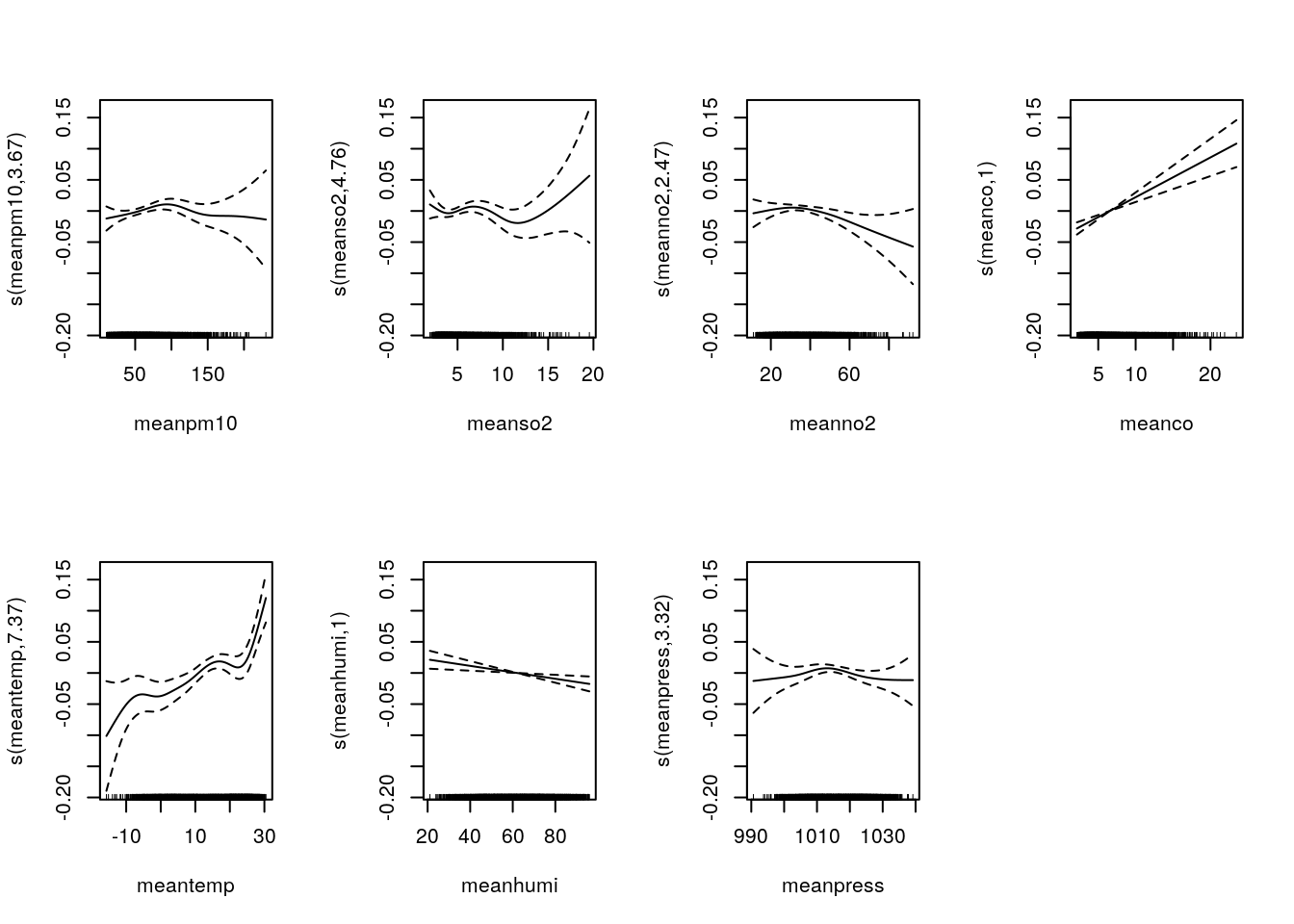

Quasipoisson

m5=gam(nonacc~offset(log(pop))+s(meanpm10) + s(meanso2) + s(meanno2) + s(meanco) + s(meantemp) + s(meanhumi)+ s(meanpress)+ season1+season2, family=quasipoisson, data=sl_pop)

summary(m5)$edf ## Effective Degree of Freedom
## [1] 2.530027 4.536262 2.253240 1.000156 7.156556 1.001500 2.974393
AIC(m5)         ## No AIC
## [1] NA
par(mfrow=c(2,4))
plot(m5)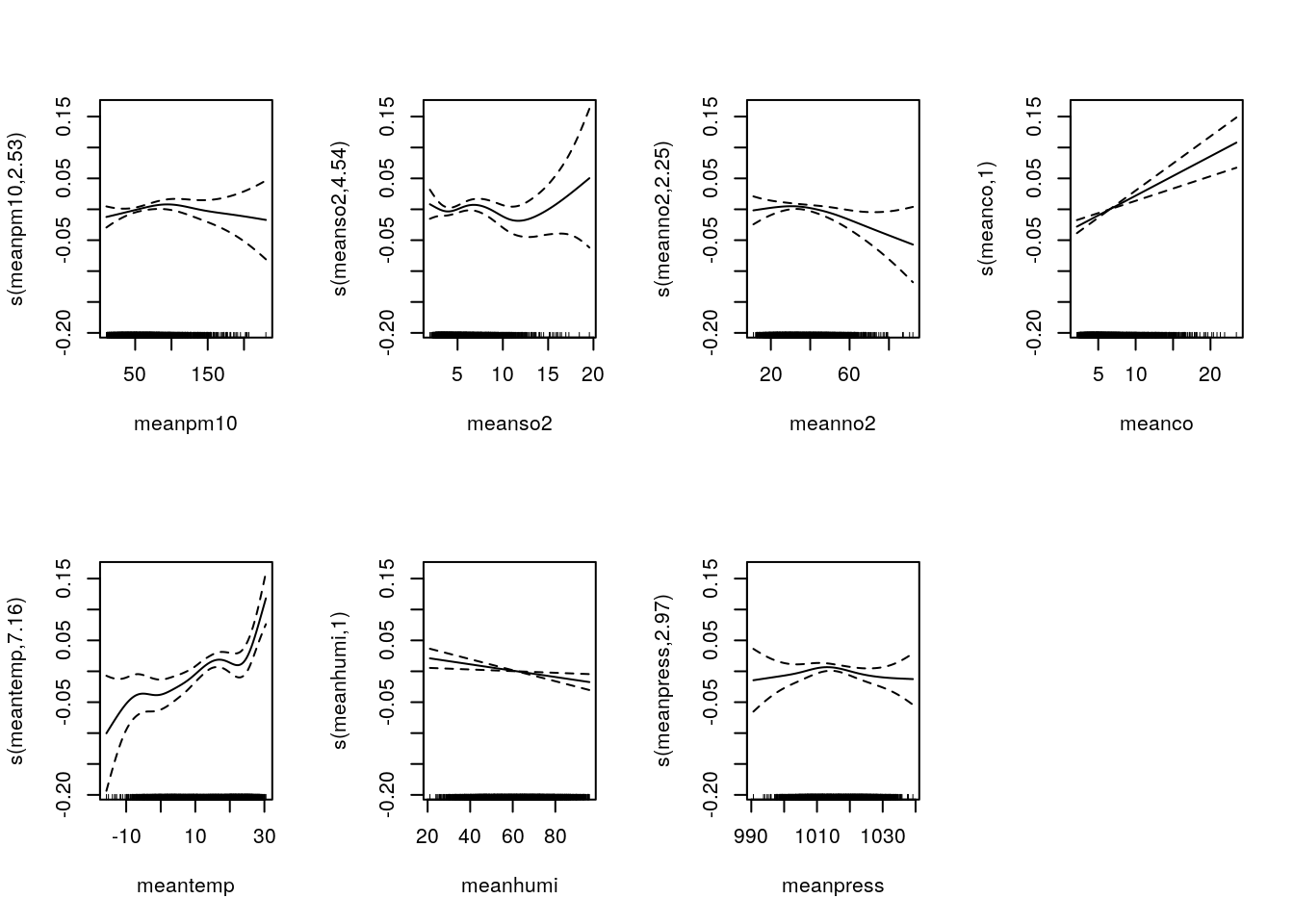

Copyright ©2016 Jinseob Kim