건강지표: DALY, QALY

GBD 2010과 DISMOD-MR의 자세한 내용은 이 슬라이드를 참고하길 바란다.

서론

미국 메이저리그에서는 세이버메트릭스(Sabermetrics)라는 분야가 대두되고 선수의 능력을 판단하는 기준으로 활발히 활용되고 있는데, 이는 야구 기록을 수리통계학적으로 분석하여 전통적인 타율, 다승, 방어율 등의 지표를 넘어 어떤 선수가 승리를 부르는 선수인지를 정확히 파악하기 위해 생긴 통계학의 한 분야이다(Albert 1997). 이와 비슷하게 집단 또는 개인의 건강지표를 숫자 하나로 표현하려는 노력들이 있었고, 현재 널리 쓰이는 것으로는 DALY(Disability Adjusted Life Year)와 QALY(Quality Adjusted Life Year)가 있다(Murray 1994; Williams, Evans, and Drummond 1987). 본문에서는 DALY와 QALY의 개념과 계산법에 대해 알아보고 어떤 공통점이 있는지, 어떤 차이점이 있는지 알아보려 한다. 특히 본문에서는 핵심적인 계산과 프로그램을 중점적으로 이야기함으로서 본 주제연구 세미나 후 바로 데이터분석을 할 수 있는 것을 목표로 한다.

DALY

DALY는 한글로 표현하면 장애보정손실연수라 할 수 있는데, 질병으로 인한 사망 또는 건강문제로 인한 손실연수를 말하는 것이다. 헷갈리면 안되는 것이, DALY는 손실정도를 측정하는 것이다. 평균기대수명으로부터 얼마나 더 손해보냐!!!를 나타내는 지표이며, 단어만 보고 잘못 추측하여 이것저것 보정하였을 때 개인 수명이 얼마나 되냐?? 를 말해주는 것이 아니라는 점을 유념하자. 흔히 DALY \(=\) YLL + YLD 로 표현하며 YLL는 years of life lost로 사망으로 인한 손실을 의미한다. 성별, 질병, 나이를 고정하였을 때 YLL은 \[\text{YLL} = \text{N}\times\text{L} \] (N: number of death, L: standard life expectancy at age of death in years) 로 표현되다. 한편 YLD는 years lost due to disability로 장해로 인한 손실을 의미하며 다음과 같이 표현된다.

\[\text{YLD} = \text{I}\times\text{DW}\times\text{L} \] (I: incidence, DW: disability weight, L: average duration of the case until remission or death(years))

Concept of DALY

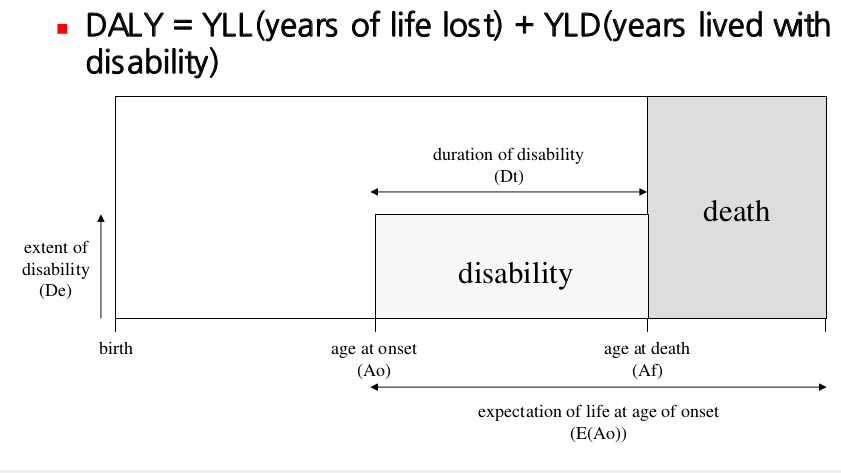
여기까지는 보건학 전공자들이 흔히 알고 있는 부분일 것이다. 자 이제 그럼 결국 DALY를 실제로 어떻게 계산하는지 알아보자. 간단히 말해서 YLL, YLD 식에 이용되는 지표들이 다 필요한 것이다(Disability weight는 후술하겠다). 성별, 연령별로 다양한 지표들이 필요한 것을 알 수 있는데 실제 모든 지표들이 완벽하게 갖추어진 경우는 거의 없다. 따라서 적절한 모형에 따라 이것을 추정해 주는 방법이 필요하고 이를 수행하는 소프트웨어가 DISMOD이다.

DISMOD

DISMOD는 Global Burden of Disease 1990에 이용된 소프트웨어로, incidence, remission, case fatality의 세 가지 지표를 이용하여 prevalence, mortality, disease duration 등의 다른 지표들을 추정하는데 이용되었다(Barendregt et al. 2003). DISMOD의 핵심은 미분방정식을 이용하여 특정 연령범위의 사람들의 건상상태를 추정하고 이를 이용하여 다른 지표들을 계산하는 것인데 그 개요는 다음과 같다.

Conceptual Disease Model

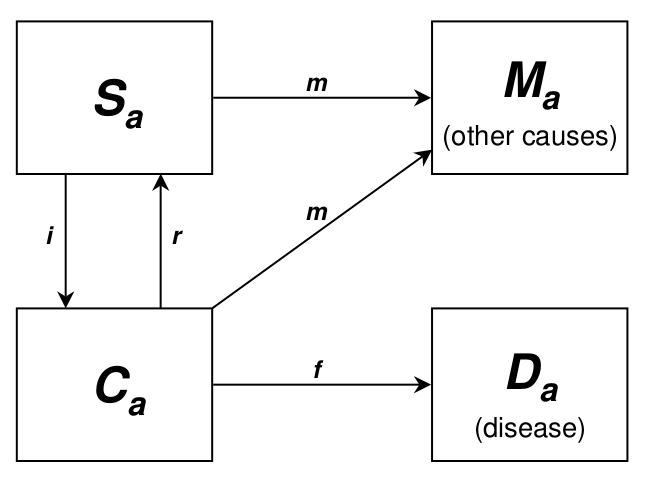
위 그림을 토대로 핵심 계산식을 표현하면 다음과 같다. \[\begin{align} \frac{dS_a}{da}&=-i_aS_a+r_aC_a\\ \frac{dC_a}{da}&=-(f_a+r_a)C_a+i_aS_a\\ \frac{dD_a}{da}&=f_aC_a \end{align}\] (\(a\): age group, \(S\): 건강한 사람의 수, \(C\): 해당 질병상태인 사람의 수, \(D\): 해당 질병으로 죽은 사람의 수, \(i\): incidence, \(r\): remission, \(f\): fatality)

첫 번째 수식을 예로 들면 건강한 사람 수의 변화량은 건강한 사람 수와 incidence의 곱만큼 감소하고 , 질병상태인 사람 수와 remission의 곱만큼 증가한다는 것이다. 이 미분방정식의 핵심은 연령별 \(i,r,f\) 를 알면 결국 \(S_a,C_a,D_a\)를 알 수 있게 된다는 것이고, 이를 알면 prevalence와 mortality 를 구할 수 있으며 이는 다음과 같다.

\[\begin{align} PY_a&=\frac{1}{2}\times (S_a+C_a+S_{a+1}+C_{a+1})\\ c_a&=\frac{1}{2}\times \frac{C_a+C_{a+1}}{PY_a}\\ b_a&=\frac{D_{a+1}-D_a}{PY_a} \end{align}\] (\(PY\): age interval person-year at risk, \(c\): prevalence, \(b\): mortality)

여기에 다른 원인으로 인한 사망률 \(m_a\)를 알고 있으면 결국, 질병상태에서 빠져나갈 확률은 \(r_a+f_a+m_a\)가 되고 이를 이용하면 disease duration또한 구할 수 있다. 정리하자면 incidence, remission, case fatality의 세 가지 지표를 토대로 나머지 지표들을 추정하는 소프트웨어가 DISMOD이다.

DISMOD II

DISMOD II는 Global Burden of Disease 2000에 이용된 소프트웨어로, DISMOD에서 부족했던 그래픽효과를 지원하며 incidence, remission, fatality의 세 지표를 input으로 받았던 한계에서 벗어나, 더 많은 질병의 상태를 추정하는데 이용할 수 있게 되었다(Barendregt et al. 2003). 즉, prevalence나 mortality 정보를 input으로 받아 역으로 다른 지표를 추정할 수 있다는 것이다. 물론 이 정보만 가지고 DISMOD의 과정을 완벽히 역으로 계산해낼 수는 없으나 각종 통계학적 방법을 이용하여 가능성이 높은 추정치를 제시하며 물론 최소 3가지 지표는 있어야 나머지도 추론할 수 있다. 한국의 질병부담에 대한 대부분의 논문들이 이 DISMOD II를 이용하였다[Yoon et al. (2007);park2006burden;yoon2002estimation].

DISMOD-MR

DISMOD-MR은 Global Burden of Disease 2010에 이용된 소프트웨어로, 여기에서 소스코드를 다운로드 받을 수 있다. 파이썬(python)에서 작동되어 진입장벽이 높으며, 베이지안 통계를 적용한 것과 Meta-regression을 수행할 수 있다는 점이 DISMOD-II와의 가장 큰 차이점이다.다(Vos et al. 2013).

베이지안 접근법의 핵심은 연구자가 관심있는 변수의 사후분포(posterior)가 사전분포(prior)와 가능도(likelihood)의 곱에 비례한다는 점인데, 기존 통계방법이 귀무가설로 변수값을 0으로 가정하고 그 가정 하에서 가능도를 최대로 하는 변수값을 계산하는 것이었다면, 베이지안 접근법은 귀무가설과 의미상 통하는 사전분포를 좀 더 유연하게 가정할 수 있다는 장점이 있다. 예를 들면 암(cancer)의 경우 일반적으로 나이가 증가할수록 incidence가 증가하는 경향이 있는데 이 양상을 사전분포(prior)로 지정한 후 데이터가 주는 정보 가능성의 정보 (likelihood)를 종합하여 판단할 수 있다는 것이다.

또 하나의 특징인 Meta-regression은 여러 지역이나 나라들의 정보를 종합하여 원하는 정보를 추정할 수 있게 하며, 이를 통하여 지역이나 나라들의 차이에 영향을 끼치는 요인을 살펴볼 수 있다. Prevalence의 예를 들어 설명하면, 각 지역별 또는 나라별로 prevalence를 모두 구한 다음 이 지표를 종속변수로 두고 회귀분석을 수행하는 것이며 지표 특성에 따라 종속변수의 분포는 로짓, 포아송, 음이항 분포 등 다양하게 지정할 수 있다.

Meta-regression에서 독립변수를 포함하는 방법은 fixed effect와 random effect가 있는데, fixed effect는 일반적인 변수(예: 성별, 나이 등)과 질병지표에 영향을 끼치리라 예상되는 지역이나 나라의 특성, study-protocol 등이 포함되어 분석될 수 있으며, random effect에는 지역이나 나라 그 자체를 변수로 두어, 지역이나 나라에 따른 heterogeniety를 살펴볼 수 있다. 베이지안 통계와 메타분석법에 대해 한글로 공부하고 싶으신 분은 Think Bayes 슬라이드 혹은 NECA 연구방법시리즈 3. 베이지안 메타분석법을 참조하길 바란다.

보정

DALY계산에 필요한 지표들을 구하는 것이 전부는 아니다. YLL = N \(\times\) L, YLD = I \(\times\) DW \(\times\) L 로 그냥 단순히 계산하는 것이 아니며, 실제로는 여러가지가 보정되는데 대표적인 것들은 다음과 같다.

연령가중치(weighting): 젊은 사람의 사망을 늙은 사람의 사망보다 더 가중치를 준다.
할인율(discounting): 현재의 건강수준을 미래의 건강수준보다 더 가중치를 준다(예: 3%)
표준기대여명

4.장애별가중치: 완벽한 건강상태를 0, 사망을 1로 가정하고 장애의 종류에 따라 PTO(person trade-off), VAS 등의 방법을 이용하여 장애별 가중치를 구함

예를 들어 3%의 할인율을 적용한다면 YLL과 YLD의 식은 다음과 같이 바뀌게 된다.(Donev et al. 2010).

\[\begin{align} \text{YLL}&=\frac{\text{N}}{0.03}(1-e^{-0.03\text{L}})\\ \text{YLD}&=\frac{\text{I}\times{DW}}{0.03}(1-e^{-0.03\text{L}}) \end{align}\]

여기에 연령가중치까지 적용하면 식은 더 복잡해지게 되며 식의 내용은 참고논문을 참조하길 바란다.

장애가중치(Disability Weight)

장애가중치 보정은 따로 이야기를 해 보겠다. 그동안 알려진 장애가중치 보정방법은 등이 있는데 이것들의 개념은 참고문헌을 참고하길 바란다[Ohnhaus and Adler (1975);McCormack et al. (1988);Crichton (2001);Bennett and Torrance (1996)}. GBD(Global burden of disease) 1996에서는 장애가중치 보정방법으로 person trade-off라는 개념을 제시하였는데(Nord 1995), 아래 그림을 보면 이해가 될 것이다.

Person trade-off

전문가집단을 대상으로 조사를 시행하였으며, 조사결과를 토대로 22개의 indicator condition을 배치하였으며 이를 7단계의 장해 범주로 나눈 후, 나머지 질병에 대해서는 구한 것을 가지고 적당히 평균을 내서 계산을 한다(아래 두 그림)

Person trade-off(2)

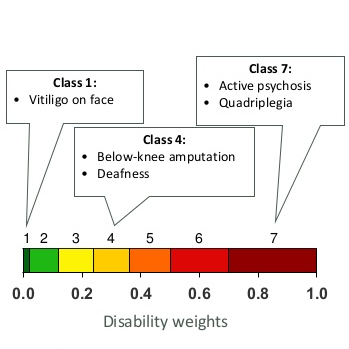
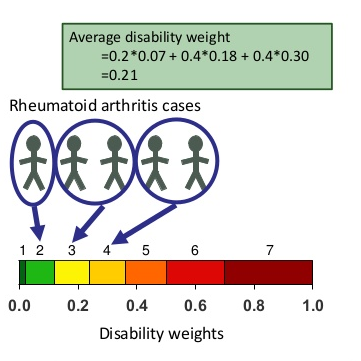
GBD 2010

GBD 2010에서는 289개의 질병과 1160개의 sequelae를 토대로 220개의 health status에 대해 가중치를 줄 수 있게 되었다(아래 그림). 전세계적으로 population-based household survey와 open-access internet survey를 시행하였으며 크게 paired comparison과 population health equivalence방법이 있다.

Disability weight in GBD 2010

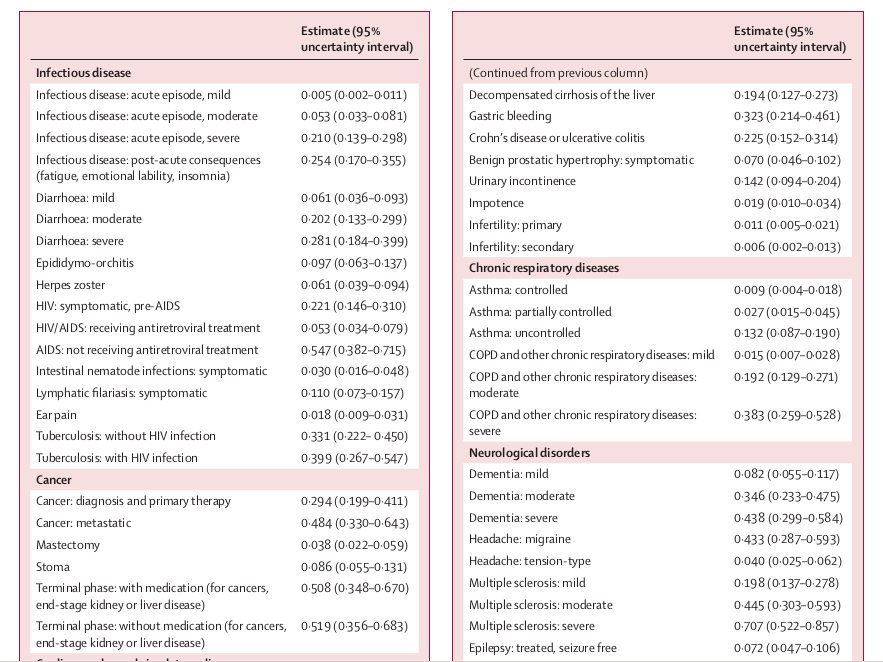
이 중 population health equivalence는 앞서 언급한 person trade-off 방법과 유사하며, paired comparison은 만성질환끼리의 비교, 급성질환끼리의 비교를 분리하여 질문하였으며 paired comparison을 통하여 질환끼리의 비교를 할 수 있으며, population health equivalence로는 어떤 질병상태와 죽음에 대한 비교를 할 수 있어 질병상태를 0-1사이의 숫자로 표현할 수 있게 해준다(Salomon et al. 2013). 이를 이용하여 paired comparison의 결과를 0-1의 scale로 변환할 수 있다.

paired comparison : 질환끼리 우열을 가린다!!
health equivalence: 각 질환이 건강에 비해 어느정도인가를 구한다. (0-1)척도
질환끼리 우열을 가린 것을 토대로 0-1척도에 대입.

QALY

QALY(Quaility Adjusted Life Year)는 삶의 질을 계량적으로 반영하기 위하여 1976년에 처음 제안된 지표로서 지금처럼 널리 쓰이게 된 것은 얼마 되지 않았는데, disease burden을 계량하기 위해 만들어진 DALY와 개념상 유사한 부분이 많다(Zeckhauser and Shepard 1976). 그냥 직관적으로 이해하고 넘어갈 사람들은 QALY는 DALY의 반대라고 알고 있으면 될 듯한데 이는 DALY에서는 완전한 상태가 0, 죽음이 1인 반면에 QALY에서는 완전한 상태를 1로 하여 기타 삶의 질의 상태를 0-1사이로 계량하는 것이기 때문이다. 허나 죽음을 1로 보는 것과 완전한 상태를 1로 하여 나머지를 측정하는 것은 개념이 상당히 달라지기 때문에 무작정 반대라고 할 수는 없으며 기타 age weighting등 세부사안에서도 차이가 난다. 기본 개념은 아래 그림에 소개되어 있으며, 본 단원에서는 QALY의 계산법에 대해 정확히 이해하고 넘어가도록 하겠다.

Concept of QALY

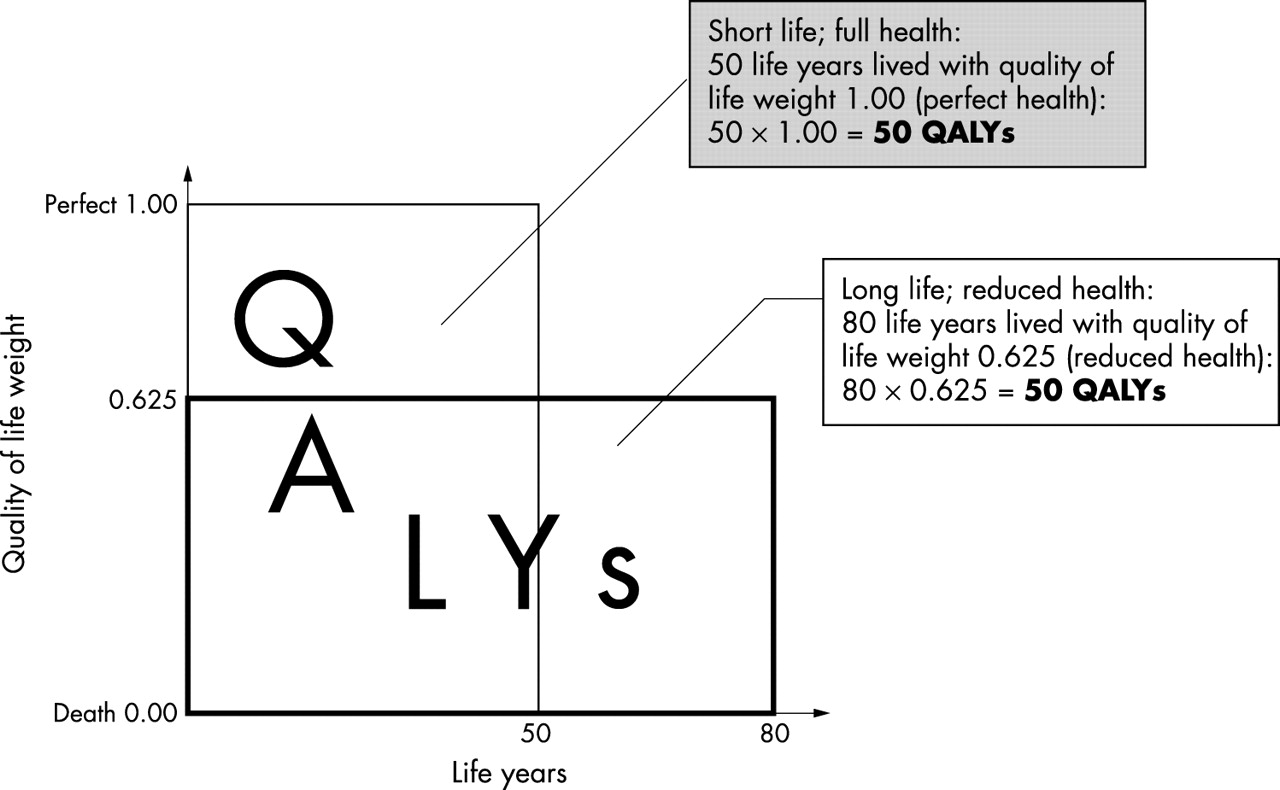
Calculation of QALY

QALY 계산에 대한 내용은 (Sassi 2006)에 자세히 나와있으며 간략히 요약해 보도록 하겠다. 어떤 사람이 Quality \(Q\)(0-1)의 상태로 1년을 산다고 하자. 그러면 그 1년동안의 QALY는

\[\begin{align} \text{QALYs lived in one year} = 1 \times Q \end{align}\] 가 되며, 따라서 어떤 사람의 \(a\)살부터의 질보정 기대여명(QALE: Quality Adjusted Life Expectancy)는 다음과 같다.

\[\begin{align} \text{QALE} = \sum_{a}^{a+L} Q_t \end{align}\] (\(L\): residual life expectancy of the individual at age \(a\), \(t\): time unit)

여기에 DALY 때처럼 discounting을 적용한다면 즉, 현재의 삶의 질에 더 가중치를 준다면

\[\begin{align} \text{Discounted QALE} = \sum_{a}^{a+L} \frac{Q_t}{(1+r)^{t-a}} \end{align}\] (\(r\): discounting rate)

가 된다. 자, 여기까지 계산할 줄 알면 개인의 QALY를 계산할 수 있는 것이다. 허나 개인의 QALY를 그냥 구하는 것으로는 별 의미가 없으며 QALY의 주 용도는 cost-effectiveness분석을 위한 것이다. 이제 특정 intervention \(i\)가 시행된 후의 quality지표를 \(Q^i\)라 하고 기존의(no intervention or standard intervention) quality 지표를 \(Q\)라 하면 QALY의 변화를

\[\begin{align} \text{QALYs gained} = \sum_{a}^{a+L^{i}} \frac{Q_t^{i}}{(1+r)^{t-a}} - \sum_{a}^{a+L} \frac{Q_t}{(1+r)^{t-a}} \end{align}\] (\(L^i\): residual life expectancy after intervention \(i\)) 로 표시할 수 있다.

DALY와의 차이점

Quality scale과 disability scale이 반대개념이 있음을 앞에서 설명하였는데, 이것 말고도 DALY와의 차이점이 있다. 대표적으로는 DALY의 weight는 전문가들이 결정하는데 비하여, QALY의 weight는 일반 인구집단에서 직접적으로 계산된다는 것이다(GBD 2010은 아님). 직접적으로 계산하는 방법에는 GBD 2010에서도 언급한 방법들이 있으며, 간접적으로 측정하는 방법에는 Health Utilities Index (Torrance et al. 1996) 나 EuroQol (Dolan 1997)이 있는데 본문에서는 EuroQol의 EQ-5D(EuroQOL five dimensions questionnaire)중 3 level 버전을 살펴보도록 하겠다[(Torrance et al. 1996; Dolan 1997; Phillips and Thompson 1998). EQ-5D-3L은 이름 그대로 5가지 차원에서 3가지 레벨로 삶의 질을 측정하겠다는 것인데 Demension은 Mobility, Pain/discomfort, Self-care, Anxiety/depression, Usual activities의 5가지가 있고 각 차원마다 삶의 질이 높은 순서대로 123으로 level이 표현된다.

Concept EQ-5D-3L

이것을 가지고 직접적인 방법인 TTO나 VAS 방법에서 나온 숫자로 변환하면 weighting이 구해지는 것이며 여러 나라들의 TTO, VAS와 EQ-5D의 상관관계에 대한 연구의 reference를 토대로 이를 변환하게 된다. 간단한 예제는 이 엑셀파일를 참조하면 된다.

개선된 QALY

QALY가 DALY와의 비교에서 큰 약점을 보이는 곳이 바로 age weighting이다. 앞서 설명한 QALY의 식에서는 age weight을 하는 부분이 없는데, 이는 젊거나 늙거나 기본적으로는 삶의 질이 차이가 없다는 가정이며 현실성이 떨어진다. 또한 discount를 보정하는 부분도 기본단위별로 discrete하게 보정되어 있어 연속함수로 보정되어 있는 DALY에 비해 부정확한 부분이다. 하나씩 해결해 보자. 먼저 discounting을 연속함수로 보정한다면 QALE는 다음과 같다. 위에서 구한 QALE와 비교해 보자.

\[\begin{align} \text{QALE} = \int_{a}^{a+L} Qe^{-r(x-a)}dx=Q\frac{1-e^{rL}}{r} \end{align}\] (\(r\): discounting rate, \(L\): residual life expectancy of the individual at age \(a\))

이에 따른 intervention \(i\)에 대한 QALEs gained는

\[\begin{align} \text{QALYs gained} = Q^i\frac{1-e^{rL^i}}{r}-Q\frac{1-e^{rL}}{r} \end{align}\] (\(i\): intervention \(i\)) 가 된다. 이제 age-weighting이 남았다. \(a\)부터 \(a+L\)살까지의 기간을 적당히 몇개의 구간으로 나누어 각 구간마다 \(Q\)값을 다르게 배정하는 것이다. 자세한 내용은 참고문헌을 살펴보길 바란다.

마치며

지금까지 건강지표의 단일수치인 DALY와 QALY를 구하는 방법에 대하여 알아보았다. 얼핏 보기에는 단 한가지 지표로 우열을 가려주는 것이 엄청난 매력으로 다가올 수 있으나, 살펴보면 가정이나 가중치를 주는 방법에 따라 결과가 천차만별로 바뀌게 되고, 데이터를 구하고 분석하는 것도 상당히 어려워 함부로 접근하기 어렵다는 생각이 들었다. 적절한 분석 소프트웨어의 부재도 문제가 되는데 특히 DISMOD-MR은 기본적으로 파이썬 프로그래밍 언어의 모듈로 실행되고 베이지안 통계의 MCMC를 위하여 다른 모듈들도 많이 설치해야 되어 윈도우에서는 설치하는 것 조차 까다로우며, 실제 다운받는 홈페이지에서도 설치하기가 쉽지 않을 것이라고 경고하고 있다. GBD 2015에 이용된 DISMOD-MR 2.1은 아예 C언어로 만들어지고 Command line으로 전 작업을 수행하게 되어 외부인이 이용하기는 더욱 어려워졌다.

DALY나 QALY의 개념 자체는 어느정도 완성되어 있어 패러다임을 바꾸는 것이 쉽지 않을 것이라 생각하나 세부 계산내용이나 쉽게 쓸수 있는 소프트웨어 개발이라는 측면에서는 아직도 연구할 부분이 무궁무진하게 많다고 생각되며, Burden of disease의 경우 출판되는 논문들의 제목과 양상이 XXX나라의 YYY질병의 Burden of disease..로 거의 천편일률화 되어 있는 것을 보아 데이터만 보유하고 DISMOD MR을 잘 사용할 수만 있으면 논문출판에도 상당히 유리한 주제라는 생각이 들었다. 마지막으로는 Disability-adjusted나 Quality-adjusted가 아닌 Desire-adjusted life year라는 개념이 중요해질 날을 꿈꾸어 본다. 어떤 종류의 욕망이든지 빠르고 쉽게, 반드시 이루어지는 것이 최고가 아닌가 생각해 본다.

참고문헌

Albert, Jim. 1997. “An Introduction to Sabermetrics.” Bowling Green State University (Http://Www-Math. Bgsu. Edu/~ Albert/Papers/Saber. Html).

Barendregt, Jan J, Gerrit J Van Oortmarssen, Theo Vos, and Christopher JL Murray. 2003. “A Generic Model for the Assessment of Disease Epidemiology: The Computational Basis of Dismod Ii.” Population Health Metrics 1 (1). BioMed Central Ltd: 4.

Bennett, KJ, and GW Torrance. 1996. “Measuring Health State Preferences and Utilities: Rating Scale, Time Trade-Off, and Standard Gamble Techniques.” Quality of Life and Pharmacoeconomics in Clinical Trials 2. Lippincott-Raven Publishers Philadelphia: 253–65.

Crichton, Nicola. 2001. “Visual Analogue Scale (Vas).” J Clin Nurs 10 (5): 706–6.

Dolan, Paul. 1997. “Modeling Valuations for Euroqol Health States.” Medical Care 35 (11). LWW: 1095–1108.

Donev, Doncho, Lijana Zaletel-Kragelj, Vesna Bjegović, and Genc Burazeri. 2010. “MEASURING the Burden of Disease: DISABILITY Adjusted Life Years (Daly).” METHODS AND TOOLS IN PUBLIC HEALTH 30: 715.

McCormack, Heather M, David J Horne, Simon Sheather, and others. 1988. “Clinical Applications of Visual Analogue Scales: A Critical Review.” Psychol Med 18 (4). Cambridge Univ Press: 1007–19.

Murray, Christopher J. 1994. “Quantifying the Burden of Disease: The Technical Basis for Disability-Adjusted Life Years.” Bulletin of the World Health Organization 72 (3). World Health Organization: 429.

Nord, Erik. 1995. “The Person-Trade-Off Approach to Valuing Health Care Programs.” Medical Decision Making 15 (3). SAGE Publications: 201–8.

Ohnhaus, Edgar E, and Rolf Adler. 1975. “Methodological Problems in the Measurement of Pain: A Comparison Between the Verbal Rating Scale and the Visual Analogue Scale.” Pain 1 (4). Elsevier: 379–84.

Phillips, Ceri, and Guy Thompson. 1998. What Is a Qaly? Vol. 1. 6. Hayward Medical Communications.

Salomon, Joshua A, Theo Vos, Daniel R Hogan, Michael Gagnon, Mohsen Naghavi, Ali Mokdad, Nazma Begum, et al. 2013. “Common Values in Assessing Health Outcomes from Disease and Injury: Disability Weights Measurement Study for the Global Burden of Disease Study 2010.” The Lancet 380 (9859). Elsevier: 2129–43.

Sassi, Franco. 2006. “Calculating Qalys, Comparing Qaly and Daly Calculations.” Health Policy and Planning 21 (5). Oxford Univ Press: 402–8.

Torrance, George W, David H Feeny, William J Furlong, Ronald D Barr, Yueming Zhang, and Qinan Wang. 1996. “Multiattribute Utility Function for a Comprehensive Health Status Classification System: Health Utilities Index Mark 2.” Medical Care 34 (7). LWW: 702–22.

Vos, Theo, Abraham D Flaxman, Mohsen Naghavi, Rafael Lozano, Catherine Michaud, Majid Ezzati, Kenji Shibuya, et al. 2013. “Years Lived with Disability (Ylds) for 1160 Sequelae of 289 Diseases and Injuries 1990–2010: A Systematic Analysis for the Global Burden of Disease Study 2010.” The Lancet 380 (9859). Elsevier: 2163–96.

Williams, Alan, RogerW Evans, and MichaelF Drummond. 1987. “Quality-Adjusted Life-Years.” The Lancet 329 (8546). Elsevier: 1372–3.

Yoon, Seok-Jun, Sang-Cheol Bae, Sang-Il Lee, Hyejung Chang, Heui Sug Jo, Joo-Hun Sung, Jae-Hyun Park, Jin-Yong Lee, and Youngsoo Shin. 2007. “Measuring the Burden of Disease in Korea.” Journal of Korean Medical Science 22 (3): 518–23.

Zeckhauser, Richard, and Donald Shepard. 1976. “Where Now for Saving Lives.” Law & Contemp. Probs. 40. HeinOnline: 5.