Advanced R (1): Fast R & Table 만들기
2018-03-13
본 자료는 아래의 내용들을 다룬다.
data.table 패키지 소개
반복문 비교:
forloop,apply문 (lapply,mapply), 멀티코어 이용(parallel 패키지의mclapply,mcmapply)Table 1 만들기: tableone 패키지
Regression result 정리하기: epiDisplay 패키지
data.table
data.table 패키지는 data step을 빠르고 쉽게 수행하기 위한 패키지로 가장 인기많은 R패키지 중 하나이다. (https://www.rdocumentation.org/trends?page1=1&sort1=direct&page2=1&sort2=total&page3=1&page4=1)
- 장점: 매우 빠르다. (base, dplyr 대비)
- 단점: 문법이 헷갈린다. (dplyr가 가장 직관적임)
Load & save data: fread & fwrite
fread 함수로 구분자 (comma, tab, …)에 상관없이 빠르게 데이터를 읽을 수 있으며, fwrtie함수로 그것을 빠르게 파일로 저장할 수 있다. GWAS result 파일을 읽고 쓰는 것을 예로 들겠다. fread로 파일을 읽으면 그 class는 data.frame에 data.table이 추가되며 문법이 원래의 data.frame과 달라지는 점을 유의하자. 만약 데이터를 빨리 읽는 것만 활용하겠다면 fread를 활용해서 읽은 후 다시 원래의 data.frame형태로 바꿔 사용하면 된다.
Code
library(rbenchmark);library(knitr)
#install.packages("data.table")
library(data.table)## Load file
setwd("/home/jinseob2kim/Dropbox/example")
df = read.table("LinearTG.assoc.linear",header=T)
dt = fread("LinearTG.assoc.linear",header=T)
## Class
class(df)## [1] "data.frame"class(dt)## [1] "data.table" "data.frame"#dt = data.table(df)
#df = data.frame(dt)
## See
dt## CHR SNP BP A1 TEST NMISS BETA STAT P
## 1: 1 rs12565286 721290 C ADD 1735 -12.760 -0.7056 4.805e-01
## 2: 1 rs12565286 721290 C sex 1735 -16.150 -2.5230 1.174e-02
## 3: 1 rs12565286 721290 C age 1735 -2.942 -6.0530 1.740e-09
## 4: 1 rs3094315 752566 G ADD 1787 6.444 1.0340 3.012e-01
## 5: 1 rs3094315 752566 G sex 1787 -16.210 -2.5840 9.851e-03
## ---
## 417071: 22 rs2238837 51212875 C sex 1787 -16.240 -2.5890 9.702e-03
## 417072: 22 rs2238837 51212875 C age 1787 -3.021 -6.3360 2.973e-10
## 417073: 22 rs28729663 51219006 A ADD 1787 1.031 0.1677 8.668e-01
## 417074: 22 rs28729663 51219006 A sex 1787 -16.250 -2.5880 9.722e-03
## 417075: 22 rs28729663 51219006 A age 1787 -3.030 -6.3500 2.718e-10## Save file
write.csv(dt, "aa.csv",row.names=F)
fwrite(dt, "aa.csv")Benchmark
setwd("/home/jinseob2kim/Dropbox/example")
## Load
kable(
benchmark(
df = read.table("LinearTG.assoc.linear",header=T),
dt = fread("LinearTG.assoc.linear",header=T), replications =1
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| df | 1 | 3.287 | 37.782 | 3.252 | 0.036 | 0 | 0 |
| dt | 1 | 0.087 | 1.000 | 0.315 | 0.000 | 0 | 0 |
## Save
kable(
benchmark(
writecsv = write.csv(dt, "aa.csv",row.names=F),
fwrite = fwrite(dt, "aa.csv"), replications =1
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child | |
|---|---|---|---|---|---|---|---|---|
| 2 | fwrite | 1 | 0.122 | 1.000 | 0.369 | 0.04 | 0 | 0 |
| 1 | writecsv | 1 | 4.450 | 36.475 | 4.309 | 0.14 | 0 | 0 |
Row opreation
data.table 의 기본 문법은 DT[i, j, by] 형태이다. https://s3.amazonaws.com/assets.datacamp.com/blog_assets/datatable_Cheat_Sheet_R.pdf 의 cheetsheet를 참고하면 좋다.

data.table 문법
Code
dt[TEST== "ADD"]## CHR SNP BP A1 TEST NMISS BETA STAT P
## 1: 1 rs12565286 721290 C ADD 1735 -12.760 -0.7056 0.4805
## 2: 1 rs3094315 752566 G ADD 1787 6.444 1.0340 0.3012
## 3: 1 rs11240777 798959 A ADD 1787 -2.710 -0.6138 0.5394
## 4: 1 rs3748597 888659 T ADD 1787 11.550 1.2200 0.2228
## 5: 1 rs2341354 918573 A ADD 1787 -3.398 -0.5769 0.5641
## ---
## 139021: 22 rs9628187 51156666 T ADD 1787 23.430 1.2820 0.1999
## 139022: 22 rs715586 51163138 T ADD 1787 2.206 0.2466 0.8053
## 139023: 22 rs3810648 51175626 G ADD 1787 -8.414 -0.5470 0.5845
## 139024: 22 rs2238837 51212875 C ADD 1787 7.657 1.6130 0.1070
## 139025: 22 rs28729663 51219006 A ADD 1787 1.031 0.1677 0.8668#dt[TEST== "ADD", ] ## same
kable(
dt[(TEST== "ADD") & (P<= 5e-8)]
)| CHR | SNP | BP | A1 | TEST | NMISS | BETA | STAT | P |
|---|---|---|---|---|---|---|---|---|
| 11 | rs1974718 | 116606766 | G | ADD | 1743 | 29.44 | 5.659 | 0 |
| 11 | rs1558860 | 116607368 | A | ADD | 1743 | 29.44 | 5.659 | 0 |
| 11 | rs1558861 | 116607437 | C | ADD | 1758 | 29.30 | 5.665 | 0 |
| 11 | rs9326246 | 116611733 | C | ADD | 1774 | 29.58 | 5.742 | 0 |
| 11 | rs180349 | 116611827 | A | ADD | 1774 | 29.30 | 5.694 | 0 |
| 11 | rs6589564 | 116624153 | C | ADD | 1736 | 29.56 | 5.657 | 0 |
| 11 | rs180326 | 116624703 | G | ADD | 1758 | 30.13 | 5.784 | 0 |
| 11 | rs7930786 | 116624727 | C | ADD | 1758 | 30.42 | 5.832 | 0 |
| 11 | rs3825041 | 116631707 | T | ADD | 1753 | 30.66 | 5.868 | 0 |
| 11 | rs10790162 | 116639104 | A | ADD | 1773 | 31.38 | 6.054 | 0 |
| 11 | rs6589565 | 116640237 | A | ADD | 1773 | 31.38 | 6.054 | 0 |
| 11 | rs2160669 | 116647607 | C | ADD | 1779 | 30.79 | 5.981 | 0 |
| 11 | rs964184 | 116648917 | G | ADD | 1779 | 30.79 | 5.981 | 0 |
| 11 | rs6589566 | 116652423 | G | ADD | 1787 | 30.92 | 6.023 | 0 |
| 11 | rs7483863 | 116652491 | A | ADD | 1782 | 30.97 | 6.022 | 0 |
| 11 | rs2075290 | 116653296 | C | ADD | 1710 | 30.64 | 5.833 | 0 |
| 11 | rs10750096 | 116656788 | C | ADD | 1777 | 31.30 | 6.074 | 0 |
| 11 | rs2266788 | 116660686 | G | ADD | 1777 | 30.72 | 5.972 | 0 |
| 11 | rs2072560 | 116661826 | T | ADD | 1735 | 30.67 | 5.842 | 0 |
| 11 | rs7123666 | 116667083 | A | ADD | 1753 | 35.18 | 5.688 | 0 |
res = dt[TEST== "ADD"]
res.df = df[df$TEST== "ADD",]
kable(
res[(CHR %in% 1:11) & (P <= 5e-8)]
)| CHR | SNP | BP | A1 | TEST | NMISS | BETA | STAT | P |
|---|---|---|---|---|---|---|---|---|
| 11 | rs1974718 | 116606766 | G | ADD | 1743 | 29.44 | 5.659 | 0 |
| 11 | rs1558860 | 116607368 | A | ADD | 1743 | 29.44 | 5.659 | 0 |
| 11 | rs1558861 | 116607437 | C | ADD | 1758 | 29.30 | 5.665 | 0 |
| 11 | rs9326246 | 116611733 | C | ADD | 1774 | 29.58 | 5.742 | 0 |
| 11 | rs180349 | 116611827 | A | ADD | 1774 | 29.30 | 5.694 | 0 |
| 11 | rs6589564 | 116624153 | C | ADD | 1736 | 29.56 | 5.657 | 0 |
| 11 | rs180326 | 116624703 | G | ADD | 1758 | 30.13 | 5.784 | 0 |
| 11 | rs7930786 | 116624727 | C | ADD | 1758 | 30.42 | 5.832 | 0 |
| 11 | rs3825041 | 116631707 | T | ADD | 1753 | 30.66 | 5.868 | 0 |
| 11 | rs10790162 | 116639104 | A | ADD | 1773 | 31.38 | 6.054 | 0 |
| 11 | rs6589565 | 116640237 | A | ADD | 1773 | 31.38 | 6.054 | 0 |
| 11 | rs2160669 | 116647607 | C | ADD | 1779 | 30.79 | 5.981 | 0 |
| 11 | rs964184 | 116648917 | G | ADD | 1779 | 30.79 | 5.981 | 0 |
| 11 | rs6589566 | 116652423 | G | ADD | 1787 | 30.92 | 6.023 | 0 |
| 11 | rs7483863 | 116652491 | A | ADD | 1782 | 30.97 | 6.022 | 0 |
| 11 | rs2075290 | 116653296 | C | ADD | 1710 | 30.64 | 5.833 | 0 |
| 11 | rs10750096 | 116656788 | C | ADD | 1777 | 31.30 | 6.074 | 0 |
| 11 | rs2266788 | 116660686 | G | ADD | 1777 | 30.72 | 5.972 | 0 |
| 11 | rs2072560 | 116661826 | T | ADD | 1735 | 30.67 | 5.842 | 0 |
| 11 | rs7123666 | 116667083 | A | ADD | 1753 | 35.18 | 5.688 | 0 |
미리 key들을 지정하면 그것들에 대해 더 빠르게 검색할 수 있다.
# 1 key
setkey(dt, TEST)
dt["ADD"]## CHR SNP BP A1 TEST NMISS BETA STAT P
## 1: 1 rs12565286 721290 C ADD 1735 -12.760 -0.7056 0.4805
## 2: 1 rs3094315 752566 G ADD 1787 6.444 1.0340 0.3012
## 3: 1 rs11240777 798959 A ADD 1787 -2.710 -0.6138 0.5394
## 4: 1 rs3748597 888659 T ADD 1787 11.550 1.2200 0.2228
## 5: 1 rs2341354 918573 A ADD 1787 -3.398 -0.5769 0.5641
## ---
## 139021: 22 rs9628187 51156666 T ADD 1787 23.430 1.2820 0.1999
## 139022: 22 rs715586 51163138 T ADD 1787 2.206 0.2466 0.8053
## 139023: 22 rs3810648 51175626 G ADD 1787 -8.414 -0.5470 0.5845
## 139024: 22 rs2238837 51212875 C ADD 1787 7.657 1.6130 0.1070
## 139025: 22 rs28729663 51219006 A ADD 1787 1.031 0.1677 0.8668## 2 keys
setkey(dt, TEST, CHR)
dt[ .("ADD", 11)] ## CHR SNP BP A1 TEST NMISS BETA STAT P
## 1: 11 rs7930823 206767 A ADD 1787 -3.401 -0.7011 0.48330
## 2: 11 rs11246002 211447 A ADD 1787 -1.714 -0.2427 0.80830
## 3: 11 rs3825075 217140 C ADD 1787 3.479 0.7614 0.44650
## 4: 11 rs536715 230368 T ADD 1787 -2.431 -0.5473 0.58430
## 5: 11 rs4980329 232598 T ADD 1787 13.300 2.0130 0.04429
## ---
## 29754: 11 rs7929069 134932565 A ADD 1787 7.046 1.1610 0.24570
## 29755: 11 rs10894957 134933513 C ADD 1787 7.179 1.4890 0.13660
## 29756: 11 rs10894958 134933972 G ADD 1787 8.607 1.4150 0.15730
## 29757: 11 rs12294124 134934063 G ADD 1787 8.363 1.3780 0.16820
## 29758: 11 rs4430531 134942626 A ADD 1787 -2.207 -0.4704 0.63810dt[ .("ADD", 1:11)]## CHR SNP BP A1 TEST NMISS BETA STAT P
## 1: 1 rs12565286 721290 C ADD 1735 -12.760 -0.7056 0.4805
## 2: 1 rs3094315 752566 G ADD 1787 6.444 1.0340 0.3012
## 3: 1 rs11240777 798959 A ADD 1787 -2.710 -0.6138 0.5394
## 4: 1 rs3748597 888659 T ADD 1787 11.550 1.2200 0.2228
## 5: 1 rs2341354 918573 A ADD 1787 -3.398 -0.5769 0.5641
## ---
## 102255: 11 rs7929069 134932565 A ADD 1787 7.046 1.1610 0.2457
## 102256: 11 rs10894957 134933513 C ADD 1787 7.179 1.4890 0.1366
## 102257: 11 rs10894958 134933972 G ADD 1787 8.607 1.4150 0.1573
## 102258: 11 rs12294124 134934063 G ADD 1787 8.363 1.3780 0.1682
## 102259: 11 rs4430531 134942626 A ADD 1787 -2.207 -0.4704 0.6381benchmark
kable(
benchmark(
res.df = df[df$TEST=="ADD",],
res = dt[TEST=="ADD"],
res.key = dt["ADD"], replications=10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child | |
|---|---|---|---|---|---|---|---|---|
| 2 | res | 10 | 0.076 | 1.000 | 0.299 | 0.000 | 0 | 0 |
| 1 | res.df | 10 | 0.182 | 2.395 | 0.170 | 0.012 | 0 | 0 |
| 3 | res.key | 10 | 0.170 | 2.237 | 0.670 | 0.000 | 0 | 0 |
Column opereation
열을 선택하는 방법도 기존의 data.frame과 비슷하나 몇 가지 차이점이 있다.
Code
res[, "SNP"] ## data.table class## SNP
## 1: rs12565286
## 2: rs3094315
## 3: rs11240777
## 4: rs3748597
## 5: rs2341354
## ---
## 139021: rs9628187
## 139022: rs715586
## 139023: rs3810648
## 139024: rs2238837
## 139025: rs28729663res[, .(SNP)] ## same## SNP
## 1: rs12565286
## 2: rs3094315
## 3: rs11240777
## 4: rs3748597
## 5: rs2341354
## ---
## 139021: rs9628187
## 139022: rs715586
## 139023: rs3810648
## 139024: rs2238837
## 139025: rs28729663res[, SNP] ## vectorres[, c("SNP","P")]## SNP P
## 1: rs12565286 0.4805
## 2: rs3094315 0.3012
## 3: rs11240777 0.5394
## 4: rs3748597 0.2228
## 5: rs2341354 0.5641
## ---
## 139021: rs9628187 0.1999
## 139022: rs715586 0.8053
## 139023: rs3810648 0.5845
## 139024: rs2238837 0.1070
## 139025: rs28729663 0.8668res[, .(SNP, P)]## SNP P
## 1: rs12565286 0.4805
## 2: rs3094315 0.3012
## 3: rs11240777 0.5394
## 4: rs3748597 0.2228
## 5: rs2341354 0.5641
## ---
## 139021: rs9628187 0.1999
## 139022: rs715586 0.8053
## 139023: rs3810648 0.5845
## 139024: rs2238837 0.1070
## 139025: rs28729663 0.8668res[, c(3, 9)]## BP P
## 1: 721290 0.4805
## 2: 752566 0.3012
## 3: 798959 0.5394
## 4: 888659 0.2228
## 5: 918573 0.5641
## ---
## 139021: 51156666 0.1999
## 139022: 51163138 0.8053
## 139023: 51175626 0.5845
## 139024: 51212875 0.1070
## 139025: 51219006 0.8668주의!!
vars= c("SNP","P")
vars = c(3,9)res[, vars] # error## Error in `[.data.table`(res, , vars): j (the 2nd argument inside [...]) is a single symbol but column name 'vars' is not found. Perhaps you intended DT[, ..vars]. This difference to data.frame is deliberate and explained in FAQ 1.1.with = F 를 뒤에 붙이거나 .SD, .SDcols 옵션을 사용하자.
res[, vars, with=F]## BP P
## 1: 721290 0.4805
## 2: 752566 0.3012
## 3: 798959 0.5394
## 4: 888659 0.2228
## 5: 918573 0.5641
## ---
## 139021: 51156666 0.1999
## 139022: 51163138 0.8053
## 139023: 51175626 0.5845
## 139024: 51212875 0.1070
## 139025: 51219006 0.8668res[, .SD, .SDcols = vars]## BP P
## 1: 721290 0.4805
## 2: 752566 0.3012
## 3: 798959 0.5394
## 4: 888659 0.2228
## 5: 918573 0.5641
## ---
## 139021: 51156666 0.1999
## 139022: 51163138 0.8053
## 139023: 51175626 0.5845
## 139024: 51212875 0.1070
## 139025: 51219006 0.8668변수 생성은 := 를 이용한다.
## Make 1 variable
res[, sigP:= as.numeric(P <=5e-8)]
## Make multiple variables
res[, ":=" (sigP1= as.numeric(P <=5e-8), sigP2= ifelse(P <=5e-5, 1, 0))]Benchmark
kable(
benchmark(
col.df = res.df$SNP,
col.dt = dt[, "SNP"], replications=10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| col.df | 10 | 0.000 | NA | 0.000 | 0 | 0 | 0 |
| col.dt | 10 | 0.012 | NA | 0.012 | 0 | 0 | 0 |
Function
이번에는 phenotype data를 예로 들겠다.
Code
ph = fread("/home/jinseob2kim/Dropbox/myarticle/MOR_heri/prac.phe")
kable(
tail(ph)
)| FID | ID | sex | age | DXA_total_tscore | FBS | tCholesterol | HDL | LDL | TG | Height | Weight | SittingHt | Waist | Hip | headcircum | armspan | BMI | SBP | DBP | birth | gweek | MET | total_kcal | PY | FTND | smoke | alcohol | hyperTG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R4F185PR | R4E1I08231 | 1 | 55 | -2.6 | 99 | 232 | 43 | 160 | 145 | 155.0 | 53.0 | 87.5 | 78.5 | 96.3 | 54.3 | 155.0 | 22.06 | 140 | 80 | 510809 | NA | 3696 | 2344.574 | 0.0 | NA | 1 | 1 | 0 |
| R4F200PR | R4E1I09631 | 1 | 59 | -3.8 | 96 | 236 | 52 | 149 | 171 | 149.5 | 54.0 | 83.6 | 74.5 | 93.4 | 53.4 | 142.5 | 24.16 | 166 | 96 | 471018 | 11.75125 | 5364 | 2514.242 | 0.0 | NA | 1 | 3 | 0 |
| R4F315PR | R4E1I13271 | 1 | 50 | 0.6 | 106 | 233 | 50 | 170 | 95 | 152.8 | 61.4 | 85.6 | 88.2 | 94.8 | 52.8 | 151.4 | 26.29 | 120 | 80 | 561205 | NA | 3072 | 1779.503 | 0.0 | NA | 1 | 1 | 0 |
| X1F330PR | X1E1I13751 | 1 | 51 | -0.8 | 85 | 153 | 46 | 93 | 79 | 151.6 | 54.4 | 84.1 | 77.1 | 95.4 | 54.4 | 150.5 | 23.67 | 104 | 68 | 550901 | NA | 4468 | 1729.046 | 0.0 | NA | 1 | 1 | 0 |
| X1X330PR | X1E1I13761 | 1 | 46 | -1.0 | 89 | 220 | 62 | 142 | 70 | 152.7 | 45.2 | 83.0 | 66.9 | 86.0 | 52.5 | 153.1 | 19.38 | 110 | 64 | 610708 | 6.91250 | 53892 | 1089.507 | 0.0 | NA | 1 | 3 | 0 |
| X1F342PR | X1E1I14140 | 0 | 34 | -1.2 | 96 | 199 | 52 | 133 | 165 | 169.5 | 80.5 | 92.1 | 90.1 | 101.0 | 57.8 | 168.8 | 28.01 | 111 | 64 | 721118 | NA | 807 | 1863.503 | 0.6 | 0 | 3 | 1 | 0 |
ph[, mean(LDL, na.rm=T)]## [1] 110.3517ph[, .(meanLDL= mean(LDL, na.rm=T), meanHDL= mean(HDL, na.rm=T))]## meanLDL meanHDL
## 1: 110.3517 49.99562kable(
ph[, lapply(.SD, mean, na.rm=T), .SDcols= -c(1,2)]
, digits=2
)| sex | age | DXA_total_tscore | FBS | tCholesterol | HDL | LDL | TG | Height | Weight | SittingHt | Waist | Hip | headcircum | armspan | BMI | SBP | DBP | birth | gweek | MET | total_kcal | PY | FTND | smoke | alcohol | hyperTG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.57 | 44.2 | -0.34 | 93.6 | 189.58 | 50 | 110.35 | 114.95 | 161.62 | 62.05 | 88.23 | 80.49 | 94.51 | 55.36 | 160.82 | 23.65 | 117.53 | 74.25 | 620639.4 | 111.23 | 6341.83 | 2034.19 | 5.53 | 3.37 | 1.57 | 2.33 | 0.12 |
Benchmark
data.frame에 내장함수인 colMeans을 적용한 것이 가장 좋았다.
ph.df = data.frame(ph)
kable(
benchmark(
mean.df = sapply(ph.df[,-c(1,2)], mean, na.rm=T),
mean.dt = ph[, lapply(.SD, mean, na.rm=T), .SDcols= -c(1,2)],
colmean.df = colMeans(ph.df[, -c(1,2)], na.rm=T),
colmean.dt = colMeans(ph[, -c(1,2)], na.rm=T), replications = 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child | |
|---|---|---|---|---|---|---|---|---|
| 3 | colmean.df | 10 | 0.017 | 1.417 | 0.017 | 0 | 0 | 0 |
| 4 | colmean.dt | 10 | 0.012 | 1.000 | 0.013 | 0 | 0 | 0 |
| 1 | mean.df | 10 | 0.014 | 1.167 | 0.013 | 0 | 0 | 0 |
| 2 | mean.dt | 10 | 0.026 | 2.167 | 0.026 | 0 | 0 | 0 |
By operation
By 옵션을 이용하여 그룹별로 함수를 적용할 수 있다.
Code
kable(
ph[, lapply(.SD, mean, na.rm=T), .SDcols= -c(1,2), by= sex],
caption = "1 group", digits=2
)| sex | age | DXA_total_tscore | FBS | tCholesterol | HDL | LDL | TG | Height | Weight | SittingHt | Waist | Hip | headcircum | armspan | BMI | SBP | DBP | birth | gweek | MET | total_kcal | PY | FTND | smoke | alcohol | hyperTG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 44.60 | -0.28 | 97.12 | 191.08 | 46.45 | 112.84 | 140.34 | 169.26 | 70.10 | 92.00 | 84.63 | 96.02 | 56.70 | 169.07 | 24.40 | 121.73 | 76.74 | 617077.5 | 179.74 | 7236.79 | 2141.69 | 13.98 | 3.57 | 2.20 | 2.65 | 0.19 |
| 1 | 43.95 | -0.37 | 91.36 | 188.63 | 52.25 | 108.77 | 98.80 | 156.76 | 56.93 | 85.83 | 77.86 | 93.55 | 54.52 | 155.58 | 23.18 | 114.85 | 72.67 | 622903.3 | 48.79 | 5788.15 | 1966.40 | 0.48 | 2.40 | 1.16 | 2.13 | 0.07 |
kable(
ph[, lapply(.SD, mean, na.rm=T), .SDcols= -c(1,2), by= .(sex, smoke)],
caption= "2 groups", digits=2
)| sex | smoke | age | DXA_total_tscore | FBS | tCholesterol | HDL | LDL | TG | Height | Weight | SittingHt | Waist | Hip | headcircum | armspan | BMI | SBP | DBP | birth | gweek | MET | total_kcal | PY | FTND | alcohol | hyperTG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | NA | 44.00 | -0.45 | 91.00 | 193.50 | 43.00 | 120.00 | 71.00 | 163.35 | 63.05 | 86.22 | 82.67 | 88.92 | 55.08 | 164.95 | 23.33 | 125.00 | 84.00 | 625505.0 | 42.18 | 4452.50 | 3193.08 | 10.00 | 2.00 | 3.00 | 0.00 |
| 1 | NA | 50.83 | 0.40 | 84.17 | 201.00 | 50.67 | 113.17 | 89.00 | 156.33 | 61.38 | 86.20 | 83.80 | 96.17 | 55.92 | 161.38 | 25.19 | 123.33 | 80.00 | 547135.2 | 3.36 | 4643.00 | 1681.71 | NaN | NaN | 2.00 | 0.00 |
| 1 | 1 | 44.27 | -0.37 | 91.30 | 188.90 | 51.89 | 109.34 | 99.00 | 156.72 | 57.06 | 85.83 | 77.96 | 93.65 | 54.53 | 155.55 | 23.24 | 115.16 | 72.86 | 619799.3 | 40.10 | 5778.30 | 1963.52 | 0.00 | 3.00 | 2.09 | 0.07 |
| 1 | 2 | 40.25 | -0.46 | 88.72 | 188.79 | 54.38 | 107.08 | 92.17 | 157.79 | 55.48 | 86.28 | 76.75 | 93.15 | 54.44 | 156.23 | 22.29 | 108.68 | 68.36 | 658263.9 | 41.95 | 4100.78 | 1862.11 | 5.21 | 1.72 | 2.36 | 0.09 |
| 0 | 1 | 44.67 | -0.19 | 96.12 | 185.91 | 45.79 | 111.38 | 118.78 | 169.22 | 69.94 | 91.73 | 84.25 | 96.12 | 56.58 | 169.13 | 24.35 | 122.17 | 76.66 | 616088.0 | 105.47 | 6409.90 | 2143.65 | 0.00 | NaN | 2.44 | 0.11 |
| 0 | 2 | 49.33 | -0.28 | 99.46 | 191.00 | 46.54 | 112.73 | 136.02 | 168.46 | 69.87 | 91.79 | 85.40 | 95.81 | 56.84 | 168.36 | 24.53 | 123.38 | 77.72 | 569582.4 | 167.93 | 7731.91 | 2097.88 | 19.09 | 3.17 | 2.60 | 0.17 |
| 0 | 3 | 41.79 | -0.33 | 96.34 | 194.03 | 46.78 | 113.70 | 155.29 | 169.78 | 70.35 | 92.31 | 84.40 | 96.12 | 56.68 | 169.47 | 24.36 | 120.49 | 76.18 | 645482.0 | 219.85 | 7460.72 | 2164.20 | 19.85 | 3.79 | 2.79 | 0.25 |
| 1 | 3 | 40.89 | -0.39 | 93.86 | 184.15 | 56.25 | 101.46 | 99.79 | 156.78 | 55.59 | 85.69 | 76.79 | 92.21 | 54.31 | 155.39 | 22.55 | 113.15 | 71.78 | 652766.5 | 128.71 | 6771.50 | 2075.10 | 7.06 | 2.70 | 2.67 | 0.09 |
Benchmark
R의 기본 함수인 aggregate와 비교해보자.
kable(
benchmark(
aggregate.df = aggregate(ph.df[,-c(1,2)], by= list(sex=ph.df$sex, smoke=ph.df$smoke), mean, na.rm=T),
by.dt = ph[, lapply(.SD, mean, na.rm=T), .SDcols= -c(1,2), by= .(sex, smoke)], replications = 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| aggregate.df | 10 | 0.113 | 2.756 | 0.113 | 0 | 0 | 0 |
| by.dt | 10 | 0.041 | 1.000 | 0.148 | 0 | 0 | 0 |
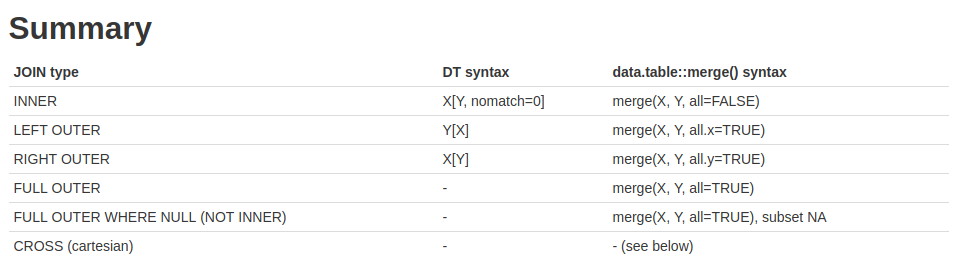
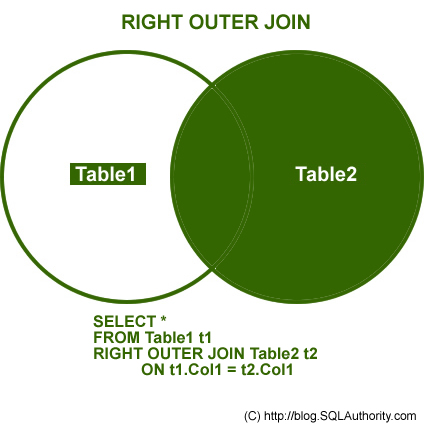
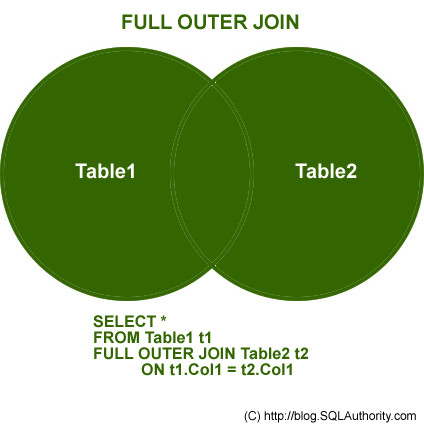
Merge
data.table에서 key를 지정하면 빠르고 간단하게 merge를 수행할 수 있다. 자세한 내용은 https://rstudio-pubs-static.s3.amazonaws.com/52230_5ae0d25125b544caab32f75f0360e775.html 를 참고하기 바란다.
Merge in data.table
두 GWAS 결과를 SNP에 따라 merge해 보자.
Code
## Set key
setkey(res, CHR,SNP,BP)
## Other GWAS result
res_logit = fread("/home/jinseob2kim/Dropbox/example/LogisticTG.assoc.logistic")[TEST=="ADD"]
setkey(res_logit, CHR,SNP,BP)
kable(
head(
res[res_logit, nomatch=0]
)
)| CHR | SNP | BP | A1 | TEST | NMISS | BETA | STAT | P | sigP | sigP1 | sigP2 | i.A1 | i.TEST | i.NMISS | OR | i.STAT | i.P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | rs1000085 | 66857915 | C | ADD | 1787 | 3.2200 | 0.3273 | 0.7434 | 0 | 0 | 0 | C | ADD | 1787 | 1.1000 | 0.57430 | 0.56570 |
| 1 | rs1000283 | 209894661 | A | ADD | 1787 | 3.8700 | 0.5782 | 0.5632 | 0 | 0 | 0 | A | ADD | 1787 | 0.7977 | -1.88000 | 0.06013 |
| 1 | rs1000382 | 175866321 | G | ADD | 1787 | 5.7340 | 1.2270 | 0.2202 | 0 | 0 | 0 | G | ADD | 1787 | 0.9781 | -0.27550 | 0.78290 |
| 1 | rs1000528 | 114471189 | C | ADD | 1787 | -5.8730 | -0.9411 | 0.3468 | 0 | 0 | 0 | C | ADD | 1787 | 0.9293 | -0.67490 | 0.49970 |
| 1 | rs1000997 | 16125961 | G | ADD | 1787 | -4.2490 | -0.9021 | 0.3671 | 0 | 0 | 0 | G | ADD | 1787 | 0.9210 | -1.01200 | 0.31160 |
| 1 | rs1001450 | 39050786 | C | ADD | 1787 | -0.9856 | -0.2140 | 0.8306 | 0 | 0 | 0 | C | ADD | 1787 | 0.9976 | -0.03037 | 0.97580 |
## Left: res, Right: res_logit
kable(
head(
res_logit[res]
)
)| CHR | SNP | BP | A1 | TEST | NMISS | OR | STAT | P | i.A1 | i.TEST | i.NMISS | BETA | i.STAT | i.P | sigP | sigP1 | sigP2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | rs1000085 | 66857915 | C | ADD | 1787 | 1.1000 | 0.57430 | 0.56570 | C | ADD | 1787 | 3.2200 | 0.3273 | 0.7434 | 0 | 0 | 0 |
| 1 | rs1000283 | 209894661 | A | ADD | 1787 | 0.7977 | -1.88000 | 0.06013 | A | ADD | 1787 | 3.8700 | 0.5782 | 0.5632 | 0 | 0 | 0 |
| 1 | rs1000382 | 175866321 | G | ADD | 1787 | 0.9781 | -0.27550 | 0.78290 | G | ADD | 1787 | 5.7340 | 1.2270 | 0.2202 | 0 | 0 | 0 |
| 1 | rs1000528 | 114471189 | C | ADD | 1787 | 0.9293 | -0.67490 | 0.49970 | C | ADD | 1787 | -5.8730 | -0.9411 | 0.3468 | 0 | 0 | 0 |
| 1 | rs1000997 | 16125961 | G | ADD | 1787 | 0.9210 | -1.01200 | 0.31160 | G | ADD | 1787 | -4.2490 | -0.9021 | 0.3671 | 0 | 0 | 0 |
| 1 | rs1001450 | 39050786 | C | ADD | 1787 | 0.9976 | -0.03037 | 0.97580 | C | ADD | 1787 | -0.9856 | -0.2140 | 0.8306 | 0 | 0 | 0 |
kable(
head(
res[res_logit]
)
)| CHR | SNP | BP | A1 | TEST | NMISS | BETA | STAT | P | sigP | sigP1 | sigP2 | i.A1 | i.TEST | i.NMISS | OR | i.STAT | i.P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | rs1000085 | 66857915 | C | ADD | 1787 | 3.2200 | 0.3273 | 0.7434 | 0 | 0 | 0 | C | ADD | 1787 | 1.1000 | 0.57430 | 0.56570 |
| 1 | rs1000283 | 209894661 | A | ADD | 1787 | 3.8700 | 0.5782 | 0.5632 | 0 | 0 | 0 | A | ADD | 1787 | 0.7977 | -1.88000 | 0.06013 |
| 1 | rs1000382 | 175866321 | G | ADD | 1787 | 5.7340 | 1.2270 | 0.2202 | 0 | 0 | 0 | G | ADD | 1787 | 0.9781 | -0.27550 | 0.78290 |
| 1 | rs1000528 | 114471189 | C | ADD | 1787 | -5.8730 | -0.9411 | 0.3468 | 0 | 0 | 0 | C | ADD | 1787 | 0.9293 | -0.67490 | 0.49970 |
| 1 | rs1000997 | 16125961 | G | ADD | 1787 | -4.2490 | -0.9021 | 0.3671 | 0 | 0 | 0 | G | ADD | 1787 | 0.9210 | -1.01200 | 0.31160 |
| 1 | rs1001450 | 39050786 | C | ADD | 1787 | -0.9856 | -0.2140 | 0.8306 | 0 | 0 | 0 | C | ADD | 1787 | 0.9976 | -0.03037 | 0.97580 |
kable(
head(
merge(res, res_logit, all=T)
)
)| CHR | SNP | BP | A1.x | TEST.x | NMISS.x | BETA | STAT.x | P.x | sigP | sigP1 | sigP2 | A1.y | TEST.y | NMISS.y | OR | STAT.y | P.y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | rs1000085 | 66857915 | C | ADD | 1787 | 3.2200 | 0.3273 | 0.7434 | 0 | 0 | 0 | C | ADD | 1787 | 1.1000 | 0.57430 | 0.56570 |
| 1 | rs1000283 | 209894661 | A | ADD | 1787 | 3.8700 | 0.5782 | 0.5632 | 0 | 0 | 0 | A | ADD | 1787 | 0.7977 | -1.88000 | 0.06013 |
| 1 | rs1000382 | 175866321 | G | ADD | 1787 | 5.7340 | 1.2270 | 0.2202 | 0 | 0 | 0 | G | ADD | 1787 | 0.9781 | -0.27550 | 0.78290 |
| 1 | rs1000528 | 114471189 | C | ADD | 1787 | -5.8730 | -0.9411 | 0.3468 | 0 | 0 | 0 | C | ADD | 1787 | 0.9293 | -0.67490 | 0.49970 |
| 1 | rs1000997 | 16125961 | G | ADD | 1787 | -4.2490 | -0.9021 | 0.3671 | 0 | 0 | 0 | G | ADD | 1787 | 0.9210 | -1.01200 | 0.31160 |
| 1 | rs1001450 | 39050786 | C | ADD | 1787 | -0.9856 | -0.2140 | 0.8306 | 0 | 0 | 0 | C | ADD | 1787 | 0.9976 | -0.03037 | 0.97580 |
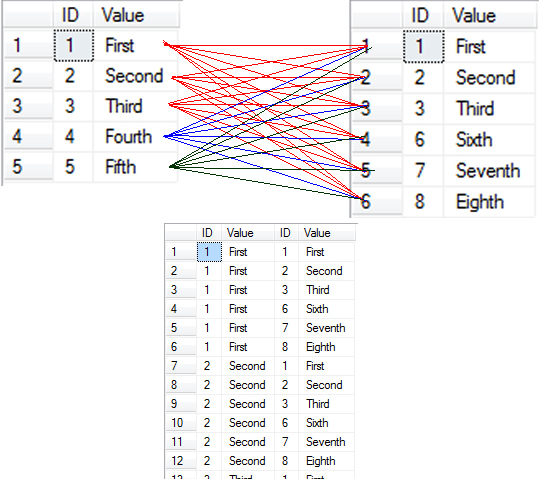
x = 1:100 ## 1~100
y = LETTERS ## A~Z
z = letters ## a~z
CJ(num= x, L= y, l= z)## num L l
## 1: 1 A a
## 2: 1 A b
## 3: 1 A c
## 4: 1 A d
## 5: 1 A e
## ---
## 67596: 100 Z v
## 67597: 100 Z w
## 67598: 100 Z x
## 67599: 100 Z y
## 67600: 100 Z zrbindlist
rbindlist함수를 사용하면 여러 개의 data를 빠르게 위아래로 합치면서 겹치지 않는 변수는 따로 분류할 수 있다.
rbindlist(list(res,res_logit), fill=T)## CHR SNP BP A1 TEST NMISS BETA STAT P sigP sigP1
## 1: 1 rs1000085 66857915 C ADD 1787 3.220 0.3273 0.7434 0 0
## 2: 1 rs1000283 209894661 A ADD 1787 3.870 0.5782 0.5632 0 0
## 3: 1 rs1000382 175866321 G ADD 1787 5.734 1.2270 0.2202 0 0
## 4: 1 rs1000528 114471189 C ADD 1787 -5.873 -0.9411 0.3468 0 0
## 5: 1 rs1000997 16125961 G ADD 1787 -4.249 -0.9021 0.3671 0 0
## ---
## 278046: 22 rs986646 22398220 C ADD 1787 NA -1.1270 0.2599 NA NA
## 278047: 22 rs9917559 37977305 A ADD 1787 NA -1.0390 0.2988 NA NA
## 278048: 22 rs9941927 40209175 G ADD 1787 NA -1.0640 0.2875 NA NA
## 278049: 22 rs9941935 22015144 G ADD 1787 NA -0.7683 0.4423 NA NA
## 278050: 22 rs999224 27834500 G ADD 1787 NA 0.6709 0.5023 NA NA
## sigP2 OR
## 1: 0 NA
## 2: 0 NA
## 3: 0 NA
## 4: 0 NA
## 5: 0 NA
## ---
## 278046: NA 0.8858
## 278047: NA 0.8992
## 278048: NA 0.8237
## 278049: NA 0.8293
## 278050: NA 1.0540#rbind(res,res_logit, fill=T)Benchmark
Inner join을 비교해보겠다.
res_logit.df = data.frame(res_logit)
kable(
benchmark(
inner.df = merge(res.df, res_logit.df, by=c("SNP","CHR","BP"), all = F),
inner.dt = res[res_logit], replications = 1
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| inner.df | 1 | 2.423 | 49.449 | 2.423 | 0 | 0 | 0 |
| inner.dt | 1 | 0.049 | 1.000 | 0.107 | 0 | 0 | 0 |
Cross join을 비교해보겠다.
kable(
benchmark(
expand.grid.df = expand.grid(num= x, L= y, l= z),
cj.dt = CJ(num= x, L= y, l= z), replications = 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child | |
|---|---|---|---|---|---|---|---|---|
| 2 | cj.dt | 10 | 0.020 | 1.00 | 0.068 | 0 | 0 | 0 |
| 1 | expand.grid.df | 10 | 0.105 | 5.25 | 0.105 | 0 | 0 | 0 |
foverlaps: Fast overlap joins
data.table 패키지의 foverlaps함수를 이용해서
Large data with small interval: ex) GWAS 결과
Small data with large interval: ex) GENE 정보
를 합칠 수 있다. 일반적인 정보는 https://rdrr.io/cran/data.table/man/foverlaps.html 를 참고하기 바란다.
## Gene info
glist_hg18 = fread("/home/jinseob2kim/Dropbox/example/glist-hg18")
names(glist_hg18) = c("chr","start","end","gene")
setkey(glist_hg18, chr, start, end) ## Set keys
kable(
head(
glist_hg18
)
)| chr | start | end | gene |
|---|---|---|---|
| 1 | 58953 | 59871 | OR4F5 |
| 1 | 357521 | 358460 | OR4F16 |
| 1 | 357521 | 358460 | OR4F29 |
| 1 | 357521 | 358460 | OR4F3 |
| 1 | 610958 | 611897 | OR4F16 |
| 1 | 610958 | 611897 | OR4F29 |
## GWAS result: make new variable for foverlaps - chr, start, end
res[, ":=" (chr=as.character(CHR), start=BP, end=BP)] ## := -make variables
## Run
addgene = foverlaps(res, glist_hg18, by.x=c("chr","start","end"), type="within", mult="first")
## See
kable(
head(
addgene
),
align="c"
)| chr | start | end | gene | CHR | SNP | BP | A1 | TEST | NMISS | BETA | STAT | P | sigP | sigP1 | sigP2 | i.start | i.end |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 66772412 | 66983356 | SGIP1 | 1 | rs1000085 | 66857915 | C | ADD | 1787 | 3.2200 | 0.3273 | 0.7434 | 0 | 0 | 0 | 66857915 | 66857915 |
| 1 | NA | NA | NA | 1 | rs1000283 | 209894661 | A | ADD | 1787 | 3.8700 | 0.5782 | 0.5632 | 0 | 0 | 0 | 209894661 | 209894661 |
| 1 | NA | NA | NA | 1 | rs1000382 | 175866321 | G | ADD | 1787 | 5.7340 | 1.2270 | 0.2202 | 0 | 0 | 0 | 175866321 | 175866321 |
| 1 | 114433436 | 114497995 | SYT6 | 1 | rs1000528 | 114471189 | C | ADD | 1787 | -5.8730 | -0.9411 | 0.3468 | 0 | 0 | 0 | 114471189 | 114471189 |
| 1 | 16046945 | 16139537 | SPEN | 1 | rs1000997 | 16125961 | G | ADD | 1787 | -4.2490 | -0.9021 | 0.3671 | 0 | 0 | 0 | 16125961 | 16125961 |
| 1 | NA | NA | NA | 1 | rs1001450 | 39050786 | C | ADD | 1787 | -0.9856 | -0.2140 | 0.8306 | 0 | 0 | 0 | 39050786 | 39050786 |
Reshape data: wide-to-long, long-to-wide
마지막으로 data 형태를 바꾸는 melt(wide to long), dcast(long to wide) 를 알아보겠다. Phenotype data에서 lipid profile들을 한 column으로 합쳐보자.
Code
ph.long = melt(ph,
measure.vars = c("tCholesterol", "HDL", "LDL", "TG"),
id.vars = c("FID","ID","sex","age"),
variable.name = "Lipid",
value.name = "value",
na.rm =F
)
ph.long## FID ID sex age Lipid value
## 1: R1F001PR R1D1I00001 0 NA tCholesterol NA
## 2: R1F001PR R1D1I00002 1 NA tCholesterol NA
## 3: R1F002PR R1D1I00004 0 NA tCholesterol NA
## 4: R1F006PR R1D1I00012 0 NA tCholesterol NA
## 5: R1F007PR R1D1I00015 0 NA tCholesterol NA
## ---
## 13840: R4F200PR R4E1I09631 1 59 TG 171
## 13841: R4F315PR R4E1I13271 1 50 TG 95
## 13842: X1F330PR X1E1I13751 1 51 TG 79
## 13843: X1X330PR X1E1I13761 1 46 TG 70
## 13844: X1F342PR X1E1I14140 0 34 TG 165이제 dcast함수를 이용해서 다시 lipid profile들을 다른 column으로 나눠보겠다.
ph.wide = dcast(ph.long,
ID + FID + sex + age ~ Lipid,
value.var = "value"
)
ph.wide = dcast(ph.long, ... ~ Lipid, value.var = "value") ## ... same
ph.wide## FID ID sex age tCholesterol HDL LDL TG
## 1: R1F001PR R1D1I00001 0 NA NA NA NA NA
## 2: R1F001PR R1D1I00002 1 NA NA NA NA NA
## 3: R1F001PR R1E1I00010 1 31 212 60 110 134
## 4: R1F001PR R1E1I00020 1 31 175 54 81 133
## 5: R1F002PR R1D1I00004 0 NA NA NA NA NA
## ---
## 3457: X1018971 R1X1I18971 1 47 181 70 83 78
## 3458: X1019000 R1X1I19000 1 35 186 64 91 60
## 3459: X1F330PR X1E1I13751 1 51 153 46 93 79
## 3460: X1F342PR X1E1I14140 0 34 199 52 133 165
## 3461: X1X330PR X1E1I13761 1 46 220 62 142 70Benchmark
data.frame에 reshape2패키지의 melt, dcast함수를 적용한 것과 비교해보겠다.
kable(
benchmark(
melt.df = melt(ph.df, measure.vars = c("tCholesterol", "HDL", "LDL", "TG"), id.vars = c("FID","ID","sex","age"), variable.name = "Lipid", value.name = "value", na.rm =F),
melt.dt = melt(ph, measure.vars = c("tCholesterol", "HDL", "LDL", "TG"), id.vars = c("FID","ID","sex","age"), variable.name = "Lipid", value.name = "value", na.rm =F),
replications = 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| melt.df | 10 | 0.012 | 2 | 0.012 | 0 | 0 | 0 |
| melt.dt | 10 | 0.006 | 1 | 0.006 | 0 | 0 | 0 |
melt.df = melt(ph.df, measure.vars = c("tCholesterol", "HDL", "LDL", "TG"), id.vars = c("FID","ID","sex","age"), variable.name = "Lipid", value.name = "value", na.rm =F)
kable(
benchmark(
dcast.df = dcast(melt.df, ... ~ Lipid, value.var = "value"),
dcast.dt = dcast(ph.long, ... ~ Lipid, value.var = "value") ,
replications = 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| dcast.df | 10 | 0.284 | 2.254 | 1.135 | 0.8 | 0 | 0 |
| dcast.dt | 10 | 0.126 | 1.000 | 0.498 | 0.0 | 0 | 0 |
기타 data.table의 장점에 대해서는 https://jangorecki.github.io/blog/2015-12-11/Solve-common-R-problems-efficiently-with-data.table.html 를 참고하기 바란다.
Faster for-loop
이번엔 for loop과 lapply, mapply 함수, 그리고 multi-core를 활용한 mclapply, mcmapply함수를 비교하여 어떤 방법이 가장 빠른지 비교해 보겠다.
다양한 phenotype과 다양한 covariate들의 조합을 회귀분석하여 계수들을 뽑아내는 것을 예로 들겠다. 먼저 아래는 종속변수 y와 독립변수 xs 를 넣으면 회귀계수를 구해주는 함수이다.
CoefExtract = function(y, xs, data=ph){
form = as.formula(paste(y, xs, sep="~"))
reg.model = lm(form, data)
return(summary(reg.model)$coefficients)
}
kable(
CoefExtract("FBS","age+sex")
)| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 82.2952398 | 1.2453403 | 66.082534 | 0 |
| age | 0.3324244 | 0.0252670 | 13.156484 | 0 |
| sex | -5.5484049 | 0.6779199 | -8.184455 | 0 |
1 loop
Phenotype: DXA_total_tscore, FBS, tCholesterol , HDL, LDL, TG, SBP, DBP
Covariate : age + sex
8개 조합
For
ybar= c("DXA_total_tscore", "FBS","tCholesterol","HDL","LDL","TG","SBP","DBP")
out=list()
for (y in ybar){
out[[length(out)+1]] = CoefExtract(y,"age+sex")
}
out## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22lapply
lapply(ybar, CoefExtract, xs="age+sex", data=ph)## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22mclapply
mclapply는 기본으로 설치된 parallel 패키지를 통해 이용할 수 있고 윈도우는 지원하지 않는다.
library(parallel)
## Setting core
ncore = detectCores()
ncore## [1] 8options(mc.cores= ncore)
options("mc.cores")## $mc.cores
## [1] 8mclapply(ybar, CoefExtract, xs="age+sex", data=ph)## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22Benchmark
kable(
benchmark(
CoefExtract.for = {out=list(); for (y in ybar){out[[length(out)+1]] = CoefExtract(y,"age+sex")}},
CoefExtract.lapply = lapply(ybar, CoefExtract, xs="age+sex", data=ph),
CoefExtract.mclapply = mclapply(ybar, CoefExtract, xs="age+sex", data=ph), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| CoefExtract.for | 10 | 0.265 | 1.480 | 0.261 | 0.004 | 0.000 | 0.000 |
| CoefExtract.lapply | 10 | 0.179 | 1.000 | 0.178 | 0.000 | 0.000 | 0.000 |
| CoefExtract.mclapply | 10 | 0.911 | 5.089 | 0.052 | 0.799 | 0.583 | 1.399 |
2 loops
Phenotype: DXA_total_tscore, FBS, tCholesterol , HDL, LDL, TG, SBP, DBP
Covariate : No, age, age + sex, age + sex + BMI, age + sex + BMI + smoke + alcohol
총 40개 조합.
ybar= c("DXA_total_tscore", "FBS","tCholesterol","HDL","LDL","TG","SBP","DBP")
xbar= c("1","age", "age + sex", "age + sex + BMI", "age + sex + BMI + smoke + alcohol ")for
out=list()
for (y in ybar){
for (xs in xbar){
out[[length(out)+1]] = CoefExtract(y, xs)
}
}
out## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.3379654 0.02503942 -13.49733 3.13349e-40
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.10698381 0.083404931 13.27240 5.366516e-39
## age -0.03268478 0.001809118 -18.06669 5.532920e-69
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.831563111 0.184102012 -4.5168605 6.545133e-06
## age -0.037572423 0.001799589 -20.8783324 7.058002e-90
## sex -0.006860562 0.048058658 -0.1427539 8.864952e-01
## BMI 0.091340414 0.007346979 12.4323778 1.502111e-34
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.73765347 0.222698896 -3.312336 9.374104e-04
## age -0.03700925 0.001883908 -19.644936 2.057143e-80
## sex -0.10272560 0.061351996 -1.674364 9.417495e-02
## BMI 0.09076497 0.007342021 12.362395 3.457890e-34
## smoke -0.11702823 0.035615571 -3.285873 1.029688e-03
## alcohol 0.05804926 0.028477854 2.038400 4.160729e-02
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 93.59679 0.3447227 271.5133 0
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 78.679816 1.17831767 66.77301 0.00000e+00
## age 0.337473 0.02556222 13.20202 1.26334e-38
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[9]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 63.9065756 2.61870235 24.403910 3.688355e-119
## age 0.2905877 0.02557697 11.361300 2.924312e-29
## sex -4.5777251 0.68200819 -6.712126 2.323673e-11
## BMI 0.8300624 0.10458434 7.936775 3.000944e-15
##
## [[10]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 60.1455518 3.17678185 18.9328555 3.377702e-75
## age 0.3037790 0.02686746 11.3065755 5.340063e-29
## sex -3.4069494 0.87293887 -3.9028499 9.737209e-05
## BMI 0.8378636 0.10485473 7.9907083 1.962289e-15
## smoke 0.8850039 0.50701065 1.7455332 8.100493e-02
## alcohol 0.3938682 0.40648983 0.9689498 3.326563e-01
##
## [[11]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 189.5825 0.6786983 279.3326 0
##
## [[12]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 162.8455571 2.33251609 69.81541 0.000000e+00
## age 0.6048822 0.05060119 11.95391 3.856016e-32
##
## [[13]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[14]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 122.7682651 5.23010885 23.4733671 3.777693e-111
## age 0.5058568 0.05108269 9.9027059 9.739034e-23
## sex 0.1797371 1.36211627 0.1319543 8.950302e-01
## BMI 1.8750125 0.20887731 8.9766214 5.073238e-19
##
## [[15]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.8944422 6.32564793 18.1632686 1.116759e-69
## age 0.5197287 0.05349883 9.7147679 5.902210e-22
## sex 3.3472580 1.73820684 1.9256960 5.424639e-02
## BMI 1.8776061 0.20878806 8.9928808 4.404104e-19
## smoke 2.8883676 1.00956597 2.8609994 4.255290e-03
## alcohol 0.3095217 0.80940766 0.3824052 7.021907e-01
##
## [[16]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 49.99562 0.2387532 209.4029 0
##
## [[17]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.4615603 0.83696720 65.070125 0.000000e+00
## age -0.1010349 0.01815702 -5.564511 2.883674e-08
##
## [[18]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[19]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.51251978 1.80567194 39.050571 1.953060e-265
## age -0.04996883 0.01763607 -2.833331 4.640359e-03
## sex 4.67683256 0.47026461 9.945108 6.462027e-23
## BMI -0.89484535 0.07211397 -12.408766 1.948859e-34
##
## [[20]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.20012687 2.17841379 29.471043 6.339215e-166
## age -0.02200388 0.01842382 -1.194317 2.324580e-01
## sex 6.05321827 0.59860014 10.112290 1.266824e-23
## BMI -0.88922960 0.07190201 -12.367243 3.205323e-34
## smoke 0.65970025 0.34767228 1.897477 5.787070e-02
## alcohol 1.31674087 0.27874217 4.723867 2.431448e-06
##
## [[21]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.3517 0.5831126 189.246 0
##
## [[22]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 85.8401109 1.99674617 42.9900 5.681223e-309
## age 0.5545365 0.04331706 12.8018 1.747137e-36
##
## [[23]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[24]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.9780380 4.44686481 10.564305 1.349740e-25
## age 0.4544901 0.04343271 10.464234 3.743974e-25
## sex -1.4772736 1.15813018 -1.275568 2.022168e-01
## BMI 1.8684460 0.17759652 10.520735 2.106848e-25
##
## [[25]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.3472610 5.38727954 9.5312041 3.317163e-21
## age 0.4204558 0.04556263 9.2280843 5.372290e-20
## sex -1.5564993 1.48035526 -1.0514364 2.931516e-01
## BMI 1.8659773 0.17781572 10.4938829 2.780782e-25
## smoke 0.7554175 0.85980348 0.8785933 3.796994e-01
## alcohol -1.6911739 0.68933734 -2.4533328 1.421622e-02
##
## [[26]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.9459 1.49712 76.77802 0
##
## [[27]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 71.8690680 5.207705 13.80053 6.224706e-42
## age 0.9746975 0.112993 8.62618 1.056875e-17
##
## [[28]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[29]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -61.8235400 10.9100869 -5.666640 1.608477e-08
## age 0.5652551 0.1065660 5.304271 1.221816e-07
## sex -32.2921274 2.8411518 -11.365858 2.783645e-29
## BMI 7.2516766 0.4356443 16.645866 2.467171e-59
##
## [[30]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -103.3730606 13.1336369 -7.870863 5.040792e-15
## age 0.6760743 0.1110898 6.085834 1.321844e-09
## sex -17.1854270 3.6089380 -4.761907 2.018190e-06
## BMI 7.3001863 0.4335010 16.840070 1.310279e-60
## smoke 13.2007428 2.0959972 6.298073 3.502561e-10
## alcohol 2.4392043 1.6806952 1.451307 1.468098e-01
##
## [[31]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.5271 0.323093 363.7563 0
##
## [[32]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 92.5662939 1.0241235 90.38587 0.000000e+00
## age 0.5647055 0.0222173 25.41738 4.329773e-128
##
## [[33]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[34]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.556786 2.20727979 31.965493 1.125800e-190
## age 0.498183 0.02155045 23.117058 4.134648e-108
## sex -5.105478 0.57474987 -8.882957 1.156815e-18
## BMI 1.186790 0.08813541 13.465533 4.635262e-40
##
## [[35]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.1220591 2.67610689 26.2030113 4.168194e-135
## age 0.4992206 0.02262375 22.0662219 2.208439e-99
## sex -5.1038772 0.73467473 -6.9471250 4.649089e-12
## BMI 1.1918429 0.08833169 13.4928123 3.311817e-40
## smoke -0.0889666 0.42679757 -0.2084515 8.348921e-01
## alcohol 0.1709080 0.34235495 0.4992129 6.176699e-01
##
## [[36]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 74.25275 0.206785 359.0818 0
##
## [[37]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.9761702 0.70502446 92.16158 0.000000e+00
## age 0.2098704 0.01529477 13.72170 1.739099e-41
##
## [[38]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22
##
## [[39]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.7850605 1.53494913 33.085826 4.392114e-202
## age 0.1674870 0.01498625 11.176048 2.191898e-28
## sex -3.0402415 0.39968282 -7.606636 3.848708e-14
## BMI 0.7577493 0.06128963 12.363417 3.348170e-34
##
## [[40]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.4465460 1.86163767 27.6351015 2.449444e-148
## age 0.1641266 0.01573824 10.4285224 5.414314e-25
## sex -3.2052800 0.51107755 -6.2716118 4.144386e-10
## BMI 0.7564303 0.06144807 12.3100741 6.315632e-34
## smoke -0.1044255 0.29690235 -0.3517166 7.250781e-01
## alcohol -0.1001832 0.23815972 -0.4206557 6.740398e-01mapply
yx.list = CJ(y= ybar, xs= xbar)
mapply(CoefExtract, yx.list[, y], yx.list[, xs], MoreArgs = list(data =ph), USE.NAMES = F)## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 74.25275 0.206785 359.0818 0
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.9761702 0.70502446 92.16158 0.000000e+00
## age 0.2098704 0.01529477 13.72170 1.739099e-41
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.7850605 1.53494913 33.085826 4.392114e-202
## age 0.1674870 0.01498625 11.176048 2.191898e-28
## sex -3.0402415 0.39968282 -7.606636 3.848708e-14
## BMI 0.7577493 0.06128963 12.363417 3.348170e-34
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.4465460 1.86163767 27.6351015 2.449444e-148
## age 0.1641266 0.01573824 10.4285224 5.414314e-25
## sex -3.2052800 0.51107755 -6.2716118 4.144386e-10
## BMI 0.7564303 0.06144807 12.3100741 6.315632e-34
## smoke -0.1044255 0.29690235 -0.3517166 7.250781e-01
## alcohol -0.1001832 0.23815972 -0.4206557 6.740398e-01
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.3379654 0.02503942 -13.49733 3.13349e-40
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.10698381 0.083404931 13.27240 5.366516e-39
## age -0.03268478 0.001809118 -18.06669 5.532920e-69
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[9]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.831563111 0.184102012 -4.5168605 6.545133e-06
## age -0.037572423 0.001799589 -20.8783324 7.058002e-90
## sex -0.006860562 0.048058658 -0.1427539 8.864952e-01
## BMI 0.091340414 0.007346979 12.4323778 1.502111e-34
##
## [[10]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.73765347 0.222698896 -3.312336 9.374104e-04
## age -0.03700925 0.001883908 -19.644936 2.057143e-80
## sex -0.10272560 0.061351996 -1.674364 9.417495e-02
## BMI 0.09076497 0.007342021 12.362395 3.457890e-34
## smoke -0.11702823 0.035615571 -3.285873 1.029688e-03
## alcohol 0.05804926 0.028477854 2.038400 4.160729e-02
##
## [[11]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 93.59679 0.3447227 271.5133 0
##
## [[12]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 78.679816 1.17831767 66.77301 0.00000e+00
## age 0.337473 0.02556222 13.20202 1.26334e-38
##
## [[13]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[14]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 63.9065756 2.61870235 24.403910 3.688355e-119
## age 0.2905877 0.02557697 11.361300 2.924312e-29
## sex -4.5777251 0.68200819 -6.712126 2.323673e-11
## BMI 0.8300624 0.10458434 7.936775 3.000944e-15
##
## [[15]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 60.1455518 3.17678185 18.9328555 3.377702e-75
## age 0.3037790 0.02686746 11.3065755 5.340063e-29
## sex -3.4069494 0.87293887 -3.9028499 9.737209e-05
## BMI 0.8378636 0.10485473 7.9907083 1.962289e-15
## smoke 0.8850039 0.50701065 1.7455332 8.100493e-02
## alcohol 0.3938682 0.40648983 0.9689498 3.326563e-01
##
## [[16]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 49.99562 0.2387532 209.4029 0
##
## [[17]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.4615603 0.83696720 65.070125 0.000000e+00
## age -0.1010349 0.01815702 -5.564511 2.883674e-08
##
## [[18]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[19]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.51251978 1.80567194 39.050571 1.953060e-265
## age -0.04996883 0.01763607 -2.833331 4.640359e-03
## sex 4.67683256 0.47026461 9.945108 6.462027e-23
## BMI -0.89484535 0.07211397 -12.408766 1.948859e-34
##
## [[20]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.20012687 2.17841379 29.471043 6.339215e-166
## age -0.02200388 0.01842382 -1.194317 2.324580e-01
## sex 6.05321827 0.59860014 10.112290 1.266824e-23
## BMI -0.88922960 0.07190201 -12.367243 3.205323e-34
## smoke 0.65970025 0.34767228 1.897477 5.787070e-02
## alcohol 1.31674087 0.27874217 4.723867 2.431448e-06
##
## [[21]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.3517 0.5831126 189.246 0
##
## [[22]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 85.8401109 1.99674617 42.9900 5.681223e-309
## age 0.5545365 0.04331706 12.8018 1.747137e-36
##
## [[23]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[24]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.9780380 4.44686481 10.564305 1.349740e-25
## age 0.4544901 0.04343271 10.464234 3.743974e-25
## sex -1.4772736 1.15813018 -1.275568 2.022168e-01
## BMI 1.8684460 0.17759652 10.520735 2.106848e-25
##
## [[25]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.3472610 5.38727954 9.5312041 3.317163e-21
## age 0.4204558 0.04556263 9.2280843 5.372290e-20
## sex -1.5564993 1.48035526 -1.0514364 2.931516e-01
## BMI 1.8659773 0.17781572 10.4938829 2.780782e-25
## smoke 0.7554175 0.85980348 0.8785933 3.796994e-01
## alcohol -1.6911739 0.68933734 -2.4533328 1.421622e-02
##
## [[26]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.5271 0.323093 363.7563 0
##
## [[27]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 92.5662939 1.0241235 90.38587 0.000000e+00
## age 0.5647055 0.0222173 25.41738 4.329773e-128
##
## [[28]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[29]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.556786 2.20727979 31.965493 1.125800e-190
## age 0.498183 0.02155045 23.117058 4.134648e-108
## sex -5.105478 0.57474987 -8.882957 1.156815e-18
## BMI 1.186790 0.08813541 13.465533 4.635262e-40
##
## [[30]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.1220591 2.67610689 26.2030113 4.168194e-135
## age 0.4992206 0.02262375 22.0662219 2.208439e-99
## sex -5.1038772 0.73467473 -6.9471250 4.649089e-12
## BMI 1.1918429 0.08833169 13.4928123 3.311817e-40
## smoke -0.0889666 0.42679757 -0.2084515 8.348921e-01
## alcohol 0.1709080 0.34235495 0.4992129 6.176699e-01
##
## [[31]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.9459 1.49712 76.77802 0
##
## [[32]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 71.8690680 5.207705 13.80053 6.224706e-42
## age 0.9746975 0.112993 8.62618 1.056875e-17
##
## [[33]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[34]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -61.8235400 10.9100869 -5.666640 1.608477e-08
## age 0.5652551 0.1065660 5.304271 1.221816e-07
## sex -32.2921274 2.8411518 -11.365858 2.783645e-29
## BMI 7.2516766 0.4356443 16.645866 2.467171e-59
##
## [[35]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -103.3730606 13.1336369 -7.870863 5.040792e-15
## age 0.6760743 0.1110898 6.085834 1.321844e-09
## sex -17.1854270 3.6089380 -4.761907 2.018190e-06
## BMI 7.3001863 0.4335010 16.840070 1.310279e-60
## smoke 13.2007428 2.0959972 6.298073 3.502561e-10
## alcohol 2.4392043 1.6806952 1.451307 1.468098e-01
##
## [[36]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 189.5825 0.6786983 279.3326 0
##
## [[37]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 162.8455571 2.33251609 69.81541 0.000000e+00
## age 0.6048822 0.05060119 11.95391 3.856016e-32
##
## [[38]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[39]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 122.7682651 5.23010885 23.4733671 3.777693e-111
## age 0.5058568 0.05108269 9.9027059 9.739034e-23
## sex 0.1797371 1.36211627 0.1319543 8.950302e-01
## BMI 1.8750125 0.20887731 8.9766214 5.073238e-19
##
## [[40]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.8944422 6.32564793 18.1632686 1.116759e-69
## age 0.5197287 0.05349883 9.7147679 5.902210e-22
## sex 3.3472580 1.73820684 1.9256960 5.424639e-02
## BMI 1.8776061 0.20878806 8.9928808 4.404104e-19
## smoke 2.8883676 1.00956597 2.8609994 4.255290e-03
## alcohol 0.3095217 0.80940766 0.3824052 7.021907e-01mcmapply
mcmapply(CoefExtract, yx.list[, y], yx.list[, xs], MoreArgs = list(data =ph), USE.NAMES = F)## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 74.25275 0.206785 359.0818 0
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.9761702 0.70502446 92.16158 0.000000e+00
## age 0.2098704 0.01529477 13.72170 1.739099e-41
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 67.5399799 0.74115994 91.127402 0.000000e+00
## age 0.2063502 0.01504109 13.719106 1.800342e-41
## sex -3.9415045 0.40350073 -9.768271 3.543069e-22
##
## [[4]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.7850605 1.53494913 33.085826 4.392114e-202
## age 0.1674870 0.01498625 11.176048 2.191898e-28
## sex -3.0402415 0.39968282 -7.606636 3.848708e-14
## BMI 0.7577493 0.06128963 12.363417 3.348170e-34
##
## [[5]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.4465460 1.86163767 27.6351015 2.449444e-148
## age 0.1641266 0.01573824 10.4285224 5.414314e-25
## sex -3.2052800 0.51107755 -6.2716118 4.144386e-10
## BMI 0.7564303 0.06144807 12.3100741 6.315632e-34
## smoke -0.1044255 0.29690235 -0.3517166 7.250781e-01
## alcohol -0.1001832 0.23815972 -0.4206557 6.740398e-01
##
## [[6]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.3379654 0.02503942 -13.49733 3.13349e-40
##
## [[7]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.10698381 0.083404931 13.27240 5.366516e-39
## age -0.03268478 0.001809118 -18.06669 5.532920e-69
##
## [[8]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.18315428 0.08920472 13.263359 6.016230e-39
## age -0.03279314 0.00180811 -18.136692 1.786053e-69
## sex -0.11623913 0.04857521 -2.392972 1.678020e-02
##
## [[9]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.831563111 0.184102012 -4.5168605 6.545133e-06
## age -0.037572423 0.001799589 -20.8783324 7.058002e-90
## sex -0.006860562 0.048058658 -0.1427539 8.864952e-01
## BMI 0.091340414 0.007346979 12.4323778 1.502111e-34
##
## [[10]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.73765347 0.222698896 -3.312336 9.374104e-04
## age -0.03700925 0.001883908 -19.644936 2.057143e-80
## sex -0.10272560 0.061351996 -1.674364 9.417495e-02
## BMI 0.09076497 0.007342021 12.362395 3.457890e-34
## smoke -0.11702823 0.035615571 -3.285873 1.029688e-03
## alcohol 0.05804926 0.028477854 2.038400 4.160729e-02
##
## [[11]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 93.59679 0.3447227 271.5133 0
##
## [[12]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 78.679816 1.17831767 66.77301 0.00000e+00
## age 0.337473 0.02556222 13.20202 1.26334e-38
##
## [[13]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 82.2952398 1.24534026 66.082534 0.000000e+00
## age 0.3324244 0.02526696 13.156484 2.230556e-38
## sex -5.5484049 0.67791988 -8.184455 4.144824e-16
##
## [[14]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 63.9065756 2.61870235 24.403910 3.688355e-119
## age 0.2905877 0.02557697 11.361300 2.924312e-29
## sex -4.5777251 0.68200819 -6.712126 2.323673e-11
## BMI 0.8300624 0.10458434 7.936775 3.000944e-15
##
## [[15]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 60.1455518 3.17678185 18.9328555 3.377702e-75
## age 0.3037790 0.02686746 11.3065755 5.340063e-29
## sex -3.4069494 0.87293887 -3.9028499 9.737209e-05
## BMI 0.8378636 0.10485473 7.9907083 1.962289e-15
## smoke 0.8850039 0.50701065 1.7455332 8.100493e-02
## alcohol 0.3938682 0.40648983 0.9689498 3.326563e-01
##
## [[16]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 49.99562 0.2387532 209.4029 0
##
## [[17]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.4615603 0.83696720 65.070125 0.000000e+00
## age -0.1010349 0.01815702 -5.564511 2.883674e-08
##
## [[18]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.72179051 0.87234943 58.14389 0.000000e+00
## age -0.09581274 0.01769928 -5.41337 6.721530e-08
## sex 5.73923189 0.47487666 12.08573 8.479426e-33
##
## [[19]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.51251978 1.80567194 39.050571 1.953060e-265
## age -0.04996883 0.01763607 -2.833331 4.640359e-03
## sex 4.67683256 0.47026461 9.945108 6.462027e-23
## BMI -0.89484535 0.07211397 -12.408766 1.948859e-34
##
## [[20]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.20012687 2.17841379 29.471043 6.339215e-166
## age -0.02200388 0.01842382 -1.194317 2.324580e-01
## sex 6.05321827 0.59860014 10.112290 1.266824e-23
## BMI -0.88922960 0.07190201 -12.367243 3.205323e-34
## smoke 0.65970025 0.34767228 1.897477 5.787070e-02
## alcohol 1.31674087 0.27874217 4.723867 2.431448e-06
##
## [[21]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.3517 0.5831126 189.246 0
##
## [[22]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 85.8401109 1.99674617 42.9900 5.681223e-309
## age 0.5545365 0.04331706 12.8018 1.747137e-36
##
## [[23]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2590834 2.13202348 41.396863 2.955579e-291
## age 0.5511586 0.04325706 12.741472 3.634198e-36
## sex -3.7122724 1.16059935 -3.198582 1.396832e-03
##
## [[24]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.9780380 4.44686481 10.564305 1.349740e-25
## age 0.4544901 0.04343271 10.464234 3.743974e-25
## sex -1.4772736 1.15813018 -1.275568 2.022168e-01
## BMI 1.8684460 0.17759652 10.520735 2.106848e-25
##
## [[25]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.3472610 5.38727954 9.5312041 3.317163e-21
## age 0.4204558 0.04556263 9.2280843 5.372290e-20
## sex -1.5564993 1.48035526 -1.0514364 2.931516e-01
## BMI 1.8659773 0.17781572 10.4938829 2.780782e-25
## smoke 0.7554175 0.85980348 0.8785933 3.796994e-01
## alcohol -1.6911739 0.68933734 -2.4533328 1.421622e-02
##
## [[26]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.5271 0.323093 363.7563 0
##
## [[27]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 92.5662939 1.0241235 90.38587 0.000000e+00
## age 0.5647055 0.0222173 25.41738 4.329773e-128
##
## [[28]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.8058195 1.07102646 90.38602 0.000000e+00
## age 0.5588847 0.02173539 25.71312 9.734928e-131
## sex -6.5176870 0.58308597 -11.17792 2.144958e-28
##
## [[29]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.556786 2.20727979 31.965493 1.125800e-190
## age 0.498183 0.02155045 23.117058 4.134648e-108
## sex -5.105478 0.57474987 -8.882957 1.156815e-18
## BMI 1.186790 0.08813541 13.465533 4.635262e-40
##
## [[30]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.1220591 2.67610689 26.2030113 4.168194e-135
## age 0.4992206 0.02262375 22.0662219 2.208439e-99
## sex -5.1038772 0.73467473 -6.9471250 4.649089e-12
## BMI 1.1918429 0.08833169 13.4928123 3.311817e-40
## smoke -0.0889666 0.42679757 -0.2084515 8.348921e-01
## alcohol 0.1709080 0.34235495 0.4992129 6.176699e-01
##
## [[31]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.9459 1.49712 76.77802 0
##
## [[32]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 71.8690680 5.207705 13.80053 6.224706e-42
## age 0.9746975 0.112993 8.62618 1.056875e-17
##
## [[33]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.5558111 5.382728 18.309639 9.882907e-71
## age 0.9367979 0.109219 8.577247 1.601135e-17
## sex -40.9188285 2.929610 -13.967331 7.083359e-43
##
## [[34]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -61.8235400 10.9100869 -5.666640 1.608477e-08
## age 0.5652551 0.1065660 5.304271 1.221816e-07
## sex -32.2921274 2.8411518 -11.365858 2.783645e-29
## BMI 7.2516766 0.4356443 16.645866 2.467171e-59
##
## [[35]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -103.3730606 13.1336369 -7.870863 5.040792e-15
## age 0.6760743 0.1110898 6.085834 1.321844e-09
## sex -17.1854270 3.6089380 -4.761907 2.018190e-06
## BMI 7.3001863 0.4335010 16.840070 1.310279e-60
## smoke 13.2007428 2.0959972 6.298073 3.502561e-10
## alcohol 2.4392043 1.6806952 1.451307 1.468098e-01
##
## [[36]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 189.5825 0.6786983 279.3326 0
##
## [[37]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 162.8455571 2.33251609 69.81541 0.000000e+00
## age 0.6048822 0.05060119 11.95391 3.856016e-32
##
## [[38]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 164.1880367 2.49414564 65.829370 0.000000e+00
## age 0.6030075 0.05060423 11.916148 5.939596e-32
## sex -2.0602344 1.35772605 -1.517415 1.292774e-01
##
## [[39]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 122.7682651 5.23010885 23.4733671 3.777693e-111
## age 0.5058568 0.05108269 9.9027059 9.739034e-23
## sex 0.1797371 1.36211627 0.1319543 8.950302e-01
## BMI 1.8750125 0.20887731 8.9766214 5.073238e-19
##
## [[40]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 114.8944422 6.32564793 18.1632686 1.116759e-69
## age 0.5197287 0.05349883 9.7147679 5.902210e-22
## sex 3.3472580 1.73820684 1.9256960 5.424639e-02
## BMI 1.8776061 0.20878806 8.9928808 4.404104e-19
## smoke 2.8883676 1.00956597 2.8609994 4.255290e-03
## alcohol 0.3095217 0.80940766 0.3824052 7.021907e-01Benchmark
kable(
benchmark(
CoefExtract.for2 = {out=list();for (y in ybar){for (xs in xbar){out[[length(out)+1]] = CoefExtract(y, xs)}}},
CoefExtract.mapply = mapply(CoefExtract, yx.list[, y], yx.list[, xs], MoreArgs = list(data =ph), USE.NAMES = F),
CoefExtract.mcmapply = mcmapply(CoefExtract, yx.list[, y], yx.list[, xs], MoreArgs = list(data =ph), USE.NAMES = F), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| CoefExtract.for2 | 10 | 1.259 | 1.247 | 1.235 | 0.024 | 0.000 | 0.000 |
| CoefExtract.mapply | 10 | 1.010 | 1.000 | 1.010 | 0.000 | 0.000 | 0.000 |
| CoefExtract.mcmapply | 10 | 1.018 | 1.008 | 0.044 | 0.708 | 1.687 | 1.718 |
When we use multi-core?
위의 결과를 요약하면 아래와 같다.
마법은 없다.
for나lapply,mapply나 비슷하다.- multi-core가 더 느릴 수도 있다.
- 간단한 작업을 조금 반복할 때 특히.
그럼 언제 multi-core가 효과적일까? \(N\)초간 정지하는 Sys.sleep함수를 통해 살펴보자.
\(N=0.0001\)
N=0.0001
kable(
benchmark(
forloop = {for(i in 1:8){Sys.sleep(N)}},
lapply = lapply(rep(N,8), Sys.sleep),
mclapply = mclapply(rep(N,8), Sys.sleep), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| forloop | 10 | 0.039 | 3.000 | 0.027 | 0.000 | 0.000 | 0.000 |
| lapply | 10 | 0.013 | 1.000 | 0.000 | 0.001 | 0.000 | 0.000 |
| mclapply | 10 | 0.591 | 45.462 | 0.011 | 0.608 | 0.086 | 1.007 |
\(N=0.001\)
N=0.001
kable(
benchmark(
forloop = {for(i in 1:8){Sys.sleep(N)}},
lapply = lapply(rep(N,8), Sys.sleep),
mclapply = mclapply(rep(N,8), Sys.sleep), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| forloop | 10 | 0.118 | 1.283 | 0.028 | 0.005 | 0.000 | 0.000 |
| lapply | 10 | 0.092 | 1.000 | 0.004 | 0.000 | 0.000 | 0.000 |
| mclapply | 10 | 0.752 | 8.174 | 0.028 | 0.680 | 0.078 | 1.288 |
\(N=0.01\)
N=0.01
kable(
benchmark(
forloop = {for(i in 1:8){Sys.sleep(N)}},
lapply = lapply(rep(N,8), Sys.sleep),
mclapply = mclapply(rep(N,8), Sys.sleep), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| forloop | 10 | 0.876 | 1.356 | 0.068 | 0.000 | 0.000 | 0.00 |
| lapply | 10 | 0.814 | 1.260 | 0.007 | 0.000 | 0.000 | 0.00 |
| mclapply | 10 | 0.646 | 1.000 | 0.021 | 0.569 | 0.057 | 1.08 |
\(N=0.1\)
N=0.1
kable(
benchmark(
forloop = {for(i in 1:8){Sys.sleep(N)}},
lapply = lapply(rep(N,8), Sys.sleep),
mclapply = mclapply(rep(N,8), Sys.sleep), replications= 10
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| forloop | 10 | 8.080 | 5.050 | 0.066 | 0.004 | 0.000 | 0.000 |
| lapply | 10 | 8.019 | 5.012 | 0.008 | 0.001 | 0.000 | 0.000 |
| mclapply | 10 | 1.600 | 1.000 | 0.050 | 0.624 | 0.107 | 1.145 |
\(N=1\)
N=1
kable(
benchmark(
forloop = {for(i in 1:8){Sys.sleep(N)}},
lapply = lapply(rep(N,8), Sys.sleep),
mclapply = mclapply(rep(N,8), Sys.sleep), replications= 1
)
)| test | replications | elapsed | relative | user.self | sys.self | user.child | sys.child |
|---|---|---|---|---|---|---|---|
| forloop | 1 | 8.011 | 7.586 | 0.004 | 0.000 | 0.000 | 0.000 |
| lapply | 1 | 8.008 | 7.583 | 0.001 | 0.000 | 0.000 | 0.000 |
| mclapply | 1 | 1.056 | 1.000 | 0.007 | 0.052 | 0.012 | 0.118 |
결론적으로 작업당 0.01초 이상이 걸리면 multi-core의 강점이 드러난다고 할 수 있겠다.
Table 1
tableone 패키지를 이용하면 간단하게 논문에 들어갈 table 1을 만들 수 있다. TG \(\ge200\) 을 기준으로 그룹을 나누어 table 1을 만들어보도록 하자. 편의상 몇가지 변수만 뽑아 결측치 없는 데이터를 만든 후 table 1을 만들겠다.
#install.packages("tableone")
library(tableone)
## Make TG variable
ph[,hyperTG := as.numeric(TG>=200)]
## Rename sex
ph[,sex:= ifelse(sex==0,"Male","Female")]
## Rename : Sex, Age
setnames(ph, c("sex", "age"), c("Sex", "Age"))
## select var
vars.tb1 = names(ph)[c(3:20,27,28)]
vars.tb1## [1] "Sex" "Age" "DXA_total_tscore" "FBS"
## [5] "tCholesterol" "HDL" "LDL" "TG"
## [9] "Height" "Weight" "SittingHt" "Waist"
## [13] "Hip" "headcircum" "armspan" "BMI"
## [17] "SBP" "DBP" "smoke" "alcohol"## Na omit
ph.omit = na.omit(ph, vars.tb1)Ctrl + C & Ctrl + V
CreatTableOne함수로 테이블을 만든 후 print명령어로 세부 옵션을 지정할 수 있다. 주요 옵션은 다음과 같다.
CreatTableOnevars: 테이블에 들어갈 변수들
strata : 그룹 변수(여러 개 가능)
factorVars: 범주형 변수들
data: 데이터
includeNA: 범주형변수에서
NA를 하나의 범주로 포함할 것인가?
tb1= CreateTableOne(vars = vars.tb1,
strata = "hyperTG",
factorVars = c("Sex","smoke","alcohol"),
data = ph.omit,
includeNA = F
)
tb1## Stratified by hyperTG
## 0 1 p test
## n 2365 321
## Sex = Male (%) 839 (35.5) 200 (62.3) <0.001
## Age (mean (SD)) 43.74 (13.00) 47.43 (13.23) <0.001
## DXA_total_tscore (mean (SD)) -0.32 (1.31) -0.55 (1.27) 0.003
## FBS (mean (SD)) 92.40 (15.93) 102.53 (28.28) <0.001
## tCholesterol (mean (SD)) 187.46 (34.64) 203.58 (37.36) <0.001
## HDL (mean (SD)) 51.22 (12.46) 41.56 (9.26) <0.001
## LDL (mean (SD)) 110.18 (30.16) 110.90 (32.91) 0.692
## TG (mean (SD)) 92.45 (40.55) 280.95 (91.61) <0.001
## Height (mean (SD)) 161.25 (8.44) 164.32 (8.34) <0.001
## Weight (mean (SD)) 60.91 (10.68) 70.05 (11.96) <0.001
## SittingHt (mean (SD)) 88.00 (4.67) 89.87 (4.50) <0.001
## Waist (mean (SD)) 79.50 (8.88) 87.35 (8.06) <0.001
## Hip (mean (SD)) 94.12 (5.67) 97.21 (5.91) <0.001
## headcircum (mean (SD)) 55.29 (3.52) 55.85 (1.85) 0.005
## armspan (mean (SD)) 160.50 (9.36) 163.20 (9.40) <0.001
## BMI (mean (SD)) 23.34 (3.15) 25.81 (3.21) <0.001
## SBP (mean (SD)) 116.27 (16.47) 126.57 (17.26) <0.001
## DBP (mean (SD)) 73.52 (10.50) 79.27 (11.64) <0.001
## smoke (%) <0.001
## 1 1621 (68.5) 135 (42.1)
## 2 282 (11.9) 54 (16.8)
## 3 462 (19.5) 132 (41.1)
## alcohol (%) 0.002
## 1 695 (29.4) 79 (24.6)
## 2 238 (10.1) 18 ( 5.6)
## 3 1432 (60.5) 224 (69.8)printnonnormal: 비모수통계를 쓸 연속 변수
exact: fisher-test를 쓸 범주형 변수
smd: standardized mean difference
cramVars: 2범주인 변수에서 2범주를 다 보여줄 변수.
zz= print(tb1,
nonnormal = c("FBS","TG"),
exact = c("Sex", "alcohol"),
smd = TRUE,
cramVars = "Sex",
printToggle=T,quote=T)## "Stratified by hyperTG"
## "" "0"
## "n" " 2365"
## "Sex = Female/Male (%)" "1526/839 (64.5/35.5) "
## "Age (mean (SD))" " 43.74 (13.00)"
## "DXA_total_tscore (mean (SD))" " -0.32 (1.31)"
## "FBS (median [IQR])" " 90.00 [85.00, 96.00]"
## "tCholesterol (mean (SD))" " 187.46 (34.64)"
## "HDL (mean (SD))" " 51.22 (12.46)"
## "LDL (mean (SD))" " 110.18 (30.16)"
## "TG (median [IQR])" " 85.00 [60.00, 120.00]"
## "Height (mean (SD))" " 161.25 (8.44)"
## "Weight (mean (SD))" " 60.91 (10.68)"
## "SittingHt (mean (SD))" " 88.00 (4.67)"
## "Waist (mean (SD))" " 79.50 (8.88)"
## "Hip (mean (SD))" " 94.12 (5.67)"
## "headcircum (mean (SD))" " 55.29 (3.52)"
## "armspan (mean (SD))" " 160.50 (9.36)"
## "BMI (mean (SD))" " 23.34 (3.15)"
## "SBP (mean (SD))" " 116.27 (16.47)"
## "DBP (mean (SD))" " 73.52 (10.50)"
## "smoke (%)" ""
## " 1" " 1621 (68.5) "
## " 2" " 282 (11.9) "
## " 3" " 462 (19.5) "
## "alcohol (%)" ""
## " 1" " 695 (29.4) "
## " 2" " 238 (10.1) "
## " 3" " 1432 (60.5) "
## "Stratified by hyperTG"
## "" "1" "p" "test"
## "n" " 321" "" ""
## "Sex = Female/Male (%)" "121/200 (37.7/62.3) " "<0.001" "exact"
## "Age (mean (SD))" " 47.43 (13.23)" "<0.001" ""
## "DXA_total_tscore (mean (SD))" " -0.55 (1.27)" " 0.003" ""
## "FBS (median [IQR])" " 95.00 [89.00, 106.00]" "<0.001" "nonnorm"
## "tCholesterol (mean (SD))" " 203.58 (37.36)" "<0.001" ""
## "HDL (mean (SD))" " 41.56 (9.26)" "<0.001" ""
## "LDL (mean (SD))" " 110.90 (32.91)" " 0.692" ""
## "TG (median [IQR])" " 251.00 [219.00, 311.00]" "<0.001" "nonnorm"
## "Height (mean (SD))" " 164.32 (8.34)" "<0.001" ""
## "Weight (mean (SD))" " 70.05 (11.96)" "<0.001" ""
## "SittingHt (mean (SD))" " 89.87 (4.50)" "<0.001" ""
## "Waist (mean (SD))" " 87.35 (8.06)" "<0.001" ""
## "Hip (mean (SD))" " 97.21 (5.91)" "<0.001" ""
## "headcircum (mean (SD))" " 55.85 (1.85)" " 0.005" ""
## "armspan (mean (SD))" " 163.20 (9.40)" "<0.001" ""
## "BMI (mean (SD))" " 25.81 (3.21)" "<0.001" ""
## "SBP (mean (SD))" " 126.57 (17.26)" "<0.001" ""
## "DBP (mean (SD))" " 79.27 (11.64)" "<0.001" ""
## "smoke (%)" "" "<0.001" ""
## " 1" " 135 (42.1) " "" ""
## " 2" " 54 (16.8) " "" ""
## " 3" " 132 (41.1) " "" ""
## "alcohol (%)" "" " 0.002" "exact"
## " 1" " 79 (24.6) " "" ""
## " 2" " 18 ( 5.6) " "" ""
## " 3" " 224 (69.8) " "" ""
## "Stratified by hyperTG"
## "" "SMD"
## "n" ""
## "Sex = Female/Male (%)" " 0.557"
## "Age (mean (SD))" " 0.281"
## "DXA_total_tscore (mean (SD))" " 0.178"
## "FBS (median [IQR])" " 0.441"
## "tCholesterol (mean (SD))" " 0.447"
## "HDL (mean (SD))" " 0.879"
## "LDL (mean (SD))" " 0.023"
## "TG (median [IQR])" " 2.661"
## "Height (mean (SD))" " 0.366"
## "Weight (mean (SD))" " 0.806"
## "SittingHt (mean (SD))" " 0.408"
## "Waist (mean (SD))" " 0.926"
## "Hip (mean (SD))" " 0.534"
## "headcircum (mean (SD))" " 0.199"
## "armspan (mean (SD))" " 0.288"
## "BMI (mean (SD))" " 0.777"
## "SBP (mean (SD))" " 0.610"
## "DBP (mean (SD))" " 0.518"
## "smoke (%)" " 0.567"
## " 1" ""
## " 2" ""
## " 3" ""
## "alcohol (%)" " 0.218"
## " 1" ""
## " 2" ""
## " 3" ""Export table
kable(
zz,
align="c",
caption="Descriptive statistics by TG",
col.names=c("TG < 200","TG ≥ 200","p","test","SMD")
)| TG < 200 | TG ≥ 200 | p | test | SMD | |
|---|---|---|---|---|---|
| “n” | 2365 | 321 | |||
| “Sex = Female/Male (%)” | 1526/839 (64.5/35.5) | 121/200 (37.7/62.3) | <0.001 | exact | 0.557 |
| “Age (mean (SD))” | 43.74 (13.00) | 47.43 (13.23) | <0.001 | 0.281 | |
| “DXA_total_tscore (mean (SD))” | -0.32 (1.31) | -0.55 (1.27) | 0.003 | 0.178 | |
| “FBS (median [IQR])” | 90.00 [85.00, 96.00] | 95.00 [89.00, 106.00] | <0.001 | nonnorm | 0.441 |
| “tCholesterol (mean (SD))” | 187.46 (34.64) | 203.58 (37.36) | <0.001 | 0.447 | |
| “HDL (mean (SD))” | 51.22 (12.46) | 41.56 (9.26) | <0.001 | 0.879 | |
| “LDL (mean (SD))” | 110.18 (30.16) | 110.90 (32.91) | 0.692 | 0.023 | |
| “TG (median [IQR])” | 85.00 [60.00, 120.00] | 251.00 [219.00, 311.00] | <0.001 | nonnorm | 2.661 |
| “Height (mean (SD))” | 161.25 (8.44) | 164.32 (8.34) | <0.001 | 0.366 | |
| “Weight (mean (SD))” | 60.91 (10.68) | 70.05 (11.96) | <0.001 | 0.806 | |
| “SittingHt (mean (SD))” | 88.00 (4.67) | 89.87 (4.50) | <0.001 | 0.408 | |
| “Waist (mean (SD))” | 79.50 (8.88) | 87.35 (8.06) | <0.001 | 0.926 | |
| “Hip (mean (SD))” | 94.12 (5.67) | 97.21 (5.91) | <0.001 | 0.534 | |
| “headcircum (mean (SD))” | 55.29 (3.52) | 55.85 (1.85) | 0.005 | 0.199 | |
| “armspan (mean (SD))” | 160.50 (9.36) | 163.20 (9.40) | <0.001 | 0.288 | |
| “BMI (mean (SD))” | 23.34 (3.15) | 25.81 (3.21) | <0.001 | 0.777 | |
| “SBP (mean (SD))” | 116.27 (16.47) | 126.57 (17.26) | <0.001 | 0.610 | |
| “DBP (mean (SD))” | 73.52 (10.50) | 79.27 (11.64) | <0.001 | 0.518 | |
| “smoke (%)” | <0.001 | 0.567 | |||
| " 1" | 1621 (68.5) | 135 (42.1) | |||
| " 2" | 282 (11.9) | 54 (16.8) | |||
| " 3" | 462 (19.5) | 132 (41.1) | |||
| “alcohol (%)” | 0.002 | exact | 0.218 | ||
| " 1" | 695 (29.4) | 79 (24.6) | |||
| " 2" | 238 (10.1) | 18 ( 5.6) | |||
| " 3" | 1432 (60.5) | 224 (69.8) |
Regression result
epiDisplay 패키지를 이용하면 회귀분석 결과를 보기 좋게 정리할 수 있고 adjust p-value와 crude p-value를 동시에 확인할 수 있다. 명령어는 아래의 4가지이다.
regress.display: Linear modellogistic.display: Logistic modelidr.display: Poisson regressioncox.display: Cox proportional hazard model
Linear regression
## Load package
library(epiDisplay)
## Pre-setting: factor variable
factorVars= c("Sex", "smoke", "alcohol")
ph[, (factorVars) := lapply(.SD, as.factor), .SDcols= factorVars]
## Linear model
m1 = lm(LDL~ Age +Sex + BMI + smoke + alcohol , data=ph)
## summary table
tb.m1 = regress.display(m1, crude=T, crude.p.value = T)
tb.m1## Linear regression predicting LDL
##
## crude coeff.(95%CI) crude P value adj. coeff.(95%CI)
## Age (cont. var.) 0.55 (0.47,0.64) < 0.001 0.43 (0.34,0.52)
##
## Sex: Male vs Female 4.06 (1.72,6.4) < 0.001 2.11 (-0.92,5.14)
##
## BMI (cont. var.) 2.29 (1.95,2.64) < 0.001 1.86 (1.51,2.21)
##
## smoke: ref.=1
## 2 2.18 (-1.34,5.71) 0.225 -1.49 (-5.45,2.48)
## 3 1.81 (-1,4.63) 0.207 1.45 (-1.92,4.83)
##
## alcohol: ref.=1
## 2 -5.22 (-9.48,-0.95) 0.017 -2.1 (-6.25,2.04)
## 3 -6.47 (-9.05,-3.89) < 0.001 -3.35 (-6.08,-0.63)
##
## P(t-test) P(F-test)
## Age (cont. var.) < 0.001 < 0.001
##
## Sex: Male vs Female 0.173 0.001
##
## BMI (cont. var.) < 0.001 < 0.001
##
## smoke: ref.=1 0.355
## 2 0.462
## 3 0.398
##
## alcohol: ref.=1 0.054
## 2 0.32
## 3 0.016
##
## No. of observations = 2728## Export table
kable(tb.m1$table[rownames(tb.m1$table) != "",], align="c", caption = tb.m1$last.lines)| crude coeff.(95%CI) | crude P value | adj. coeff.(95%CI) | P(t-test) | P(F-test) | |
|---|---|---|---|---|---|
| Age (cont. var.) | 0.55 (0.47,0.64) | < 0.001 | 0.43 (0.34,0.52) | < 0.001 | < 0.001 |
| Sex: Male vs Female | 4.06 (1.72,6.4) | < 0.001 | 2.11 (-0.92,5.14) | 0.173 | 0.001 |
| BMI (cont. var.) | 2.29 (1.95,2.64) | < 0.001 | 1.86 (1.51,2.21) | < 0.001 | < 0.001 |
| smoke: ref.=1 | 0.355 | ||||
| 2 | 2.18 (-1.34,5.71) | 0.225 | -1.49 (-5.45,2.48) | 0.462 | |
| 3 | 1.81 (-1,4.63) | 0.207 | 1.45 (-1.92,4.83) | 0.398 | |
| alcohol: ref.=1 | 0.054 | ||||
| 2 | -5.22 (-9.48,-0.95) | 0.017 | -2.1 (-6.25,2.04) | 0.32 | |
| 3 | -6.47 (-9.05,-3.89) | < 0.001 | -3.35 (-6.08,-0.63) | 0.016 |
Logistic regression
## Logistic model
m2 = glm(hyperTG~ Age +Sex + BMI + smoke + alcohol , data=ph, family=binomial)
## summary table
tb.m2 = logistic.display(m2, crude=T, crude.p.value = T)
tb.m2##
## Logistic regression predicting hyperTG
##
## crude OR(95%CI) crude P value adj. OR(95%CI)
## Age (cont. var.) 1.02 (1.01,1.03) < 0.001 1.02 (1.01,1.03)
##
## Sex: Male vs Female 2.94 (2.32,3.74) < 0.001 1.58 (1.13,2.23)
##
## BMI (cont. var.) 1.23 (1.19,1.27) < 0.001 1.21 (1.17,1.26)
##
## smoke: ref.=1
## 2 2.27 (1.62,3.18) < 0.001 1.49 (0.98,2.27)
## 3 3.34 (2.57,4.33) < 0.001 2.51 (1.76,3.59)
##
## alcohol: ref.=1
## 2 0.7 (0.42,1.18) 0.18 0.65 (0.37,1.14)
## 3 1.38 (1.05,1.81) 0.02 1.11 (0.8,1.53)
##
## P(Wald's test) P(LR-test)
## Age (cont. var.) < 0.001 < 0.001
##
## Sex: Male vs Female 0.008 0.008
##
## BMI (cont. var.) < 0.001 < 0.001
##
## smoke: ref.=1 < 0.001
## 2 0.064
## 3 < 0.001
##
## alcohol: ref.=1 0.106
## 2 0.131
## 3 0.53
##
## Log-likelihood = -872.071
## No. of observations = 2727
## AIC value = 1760.1421## Export table
kable(tb.m2$table[rownames(tb.m2$table) != "",], align="c", caption = tb.m2$last.lines)| crude OR(95%CI) | crude P value | adj. OR(95%CI) | P(Wald’s test) | P(LR-test) | |
|---|---|---|---|---|---|
| Age (cont. var.) | 1.02 (1.01,1.03) | < 0.001 | 1.02 (1.01,1.03) | < 0.001 | < 0.001 |
| Sex: Male vs Female | 2.94 (2.32,3.74) | < 0.001 | 1.58 (1.13,2.23) | 0.008 | 0.008 |
| BMI (cont. var.) | 1.23 (1.19,1.27) | < 0.001 | 1.21 (1.17,1.26) | < 0.001 | < 0.001 |
| smoke: ref.=1 | < 0.001 | ||||
| 2 | 2.27 (1.62,3.18) | < 0.001 | 1.49 (0.98,2.27) | 0.064 | |
| 3 | 3.34 (2.57,4.33) | < 0.001 | 2.51 (1.76,3.59) | < 0.001 | |
| alcohol: ref.=1 | 0.106 | ||||
| 2 | 0.7 (0.42,1.18) | 0.18 | 0.65 (0.37,1.14) | 0.131 | |
| 3 | 1.38 (1.05,1.81) | 0.02 | 1.11 (0.8,1.53) | 0.53 |
Poisson regression: 사망 데이터
## Load example data
library(HEAT);data(mort)
## Poisson regression
m3 = glm(nonacc~meantemp+ meanso2 + meanhumi, data= mort, family= poisson)
## Summary table
tb.m3 = idr.display(m3, crude=T, crude.p.value = T )tb.m3##
## Poisson regression predicting nonacc
##
## crude IDR(95%CI) crude P value
## meantemp (cont. var.) 0.9934 (0.9932,0.9937) < 0.001
##
## meanso2 (cont. var.) 1.02 (1.02,1.02) < 0.001
##
## meanhumi (cont. var.) 0.9942 (0.9941,0.9944) < 0.001
##
## adj. IDR(95%CI) P(Wald's test) P(LR-test)
## meantemp (cont. var.) 0.9978 (0.9975,0.9981) < 0.001 < 0.001
##
## meanso2 (cont. var.) 1.0079 (1.007,1.0089) < 0.001 < 0.001
##
## meanhumi (cont. var.) 0.9952 (0.995,0.9953) < 0.001 < 0.001
##
## Log-likelihood = -206421.7862
## No. of observations = 17361
## AIC value = 412851.5724## Export table
kable(tb.m3$table[rownames(tb.m3$table) != "",], align="c", caption = tb.m3$last.lines)| crude IDR(95%CI) | crude P value | adj. IDR(95%CI) | P(Wald’s test) | P(LR-test) | |
|---|---|---|---|---|---|
| meantemp (cont. var.) | 0.9934 (0.9932,0.9937) | < 0.001 | 0.9978 (0.9975,0.9981) | < 0.001 | < 0.001 |
| meanso2 (cont. var.) | 1.02 (1.02,1.02) | < 0.001 | 1.0079 (1.007,1.0089) | < 0.001 | < 0.001 |
| meanhumi (cont. var.) | 0.9942 (0.9941,0.9944) | < 0.001 | 0.9952 (0.995,0.9953) | < 0.001 | < 0.001 |
Cox: 생존분석
## Load package & example data
library(survival)
data(bladder)
## Cox model
m4 = coxph(Surv(stop, event) ~ rx + size + number, data=bladder)
## Summary table
tb.m4 = cox.display(m4, crude=T, crude.p.value = T )tb.m4## Cox's proportional hazard model on time ('stop') to event ('event')
##
## crude HR(95%CI) crude P value adj. HR(95%CI)
## rx (cont. var.) 0.64 (0.44,0.94) 0.024 0.58 (0.39,0.86)
##
## size (cont. var.) 0.91 (0.79,1.04) 0.182 0.95 (0.83,1.08)
##
## number (cont. var.) 1.2 (1.1,1.31) < 0.001 1.21 (1.11,1.33)
##
## P(Wald's test) P(LR-test)
## rx (cont. var.) 0.007 0.006
##
## size (cont. var.) 0.43 0.421
##
## number (cont. var.) < 0.001 < 0.001
##
## No. of observations = 340## Export table
kable(tb.m4$table[rownames(tb.m4$table) != "",], align="c", caption = tb.m4$last.lines)| crude HR(95%CI) | crude P value | adj. HR(95%CI) | P(Wald’s test) | P(LR-test) | |
|---|---|---|---|---|---|
| rx (cont. var.) | 0.64 (0.44,0.94) | 0.024 | 0.58 (0.39,0.86) | 0.007 | 0.006 |
| size (cont. var.) | 0.91 (0.79,1.04) | 0.182 | 0.95 (0.83,1.08) | 0.43 | 0.421 |
| number (cont. var.) | 1.2 (1.1,1.31) | < 0.001 | 1.21 (1.11,1.33) | < 0.001 | < 0.001 |
Copyright ©2016 Jinseob Kim